IT 프로그래밍/AI
선형 회귀 가중치 w와 비용함수 관계 시각화코드
기술1
2024. 9. 3. 16:19
선형 회귀 가중치 w와 비용함수 관계 시각화코드
import tensorflow as tf
import matplotlib.pyplot as plt
# 데이터 정의
X = tf.constant([1, 2, 3], dtype=tf.float32)
Y = tf.constant([1, 2, 3], dtype=tf.float32)
# 학습할 변수 정의
W = tf.Variable(initial_value=0.0, dtype=tf.float32)
# W의 값과 코스트를 저장할 리스트
W_val = []
cost_val = []
# W의 값을 변화시키면서 비용(cost) 계산
for i in range(-30, 50):
# W 값을 업데이트
W.assign(i * 0.1)
# 가설 계산
hypothesis = X * W
# 비용 함수 계산 (MSE)
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# 값을 리스트에 저장
W_val.append(W.numpy())
cost_val.append(cost.numpy())
# 결과 시각화
plt.plot(W_val, cost_val)
plt.xlabel("W")
plt.ylabel("Cost")
plt.show()X와 Y는 입력 데이터와 목표 값 데이터를 정의합니다. 여기서 X와 Y는 모두 [1,2,3]으로 설정됩니다. tf.constant를 사용해 상수 텐서를 생성하며, dtype=tf.float32는 데이터 타입을 32비트 부동 소수점으로 지정합니다.
W는 모델이 학습할 가중치를 나타냅니다. tf.Variable은 텐서플로우에서 변경 가능한 변수로, 여기서는 초기값을 0.0으로 나타냅니다.
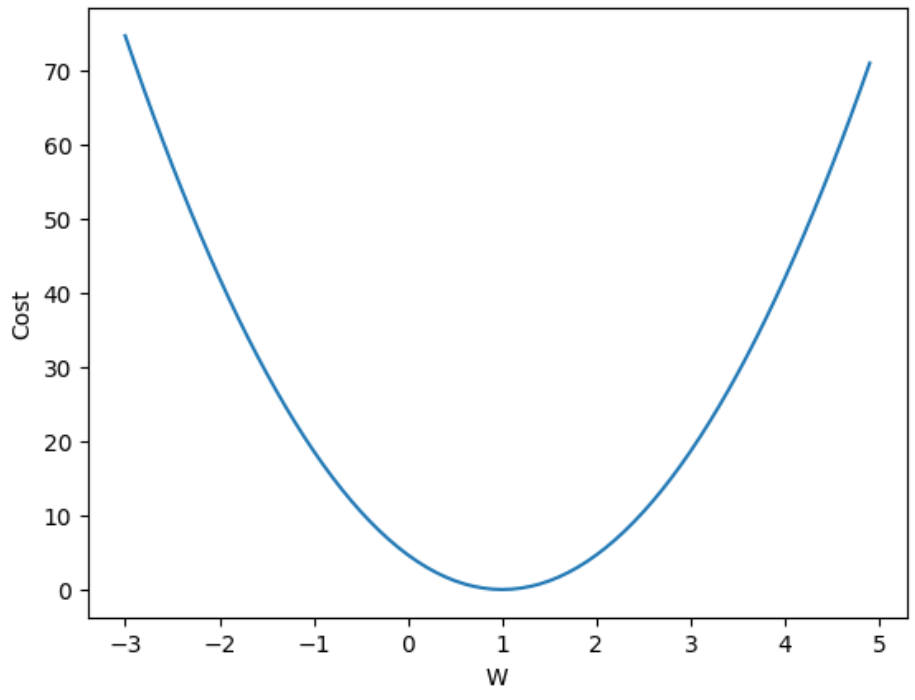
그림을 보면 알겠지만 값을 최적화하는 값은 w가 1일 때입니다.