[선형대수]

벡터의 기본적인 개념

• 공간 상의 한 화살표
• 숫자 자료의 배열 

벡터는 공간 상의 한 화살표로 표현되며, 방향과 크기를 가집니다.

수학적으로는 숫자 자료의 배열로 나타낼 수 있습니다.

 

 

• 좌표: 벡터는 한 쌍의 숫자(예: 2차원 벡터)와 일대일로 대응된다.
  • 예) v=(x,y)
• 3차원 벡터: 차원이 늘어나면 추가적인 좌표가 포함된다.
  • 예) v=(x,y,z), 여기서 z는 3차원의 축을 나타냄.

 

3차원 벡터

 

스케일(Scaling)

스케일은 벡터의 방향을 유지하면서 그 길이를 늘리거나 줄이거나 뒤집는 과정이다.

• 스케일링의 결과는 기존 벡터와 같은 방향이거나 반대 방향을 가지며, 크기가 변한다.

스칼라(Scalar)

스칼라는 벡터를 스케일하는 데 사용되는 숫자이다.

 

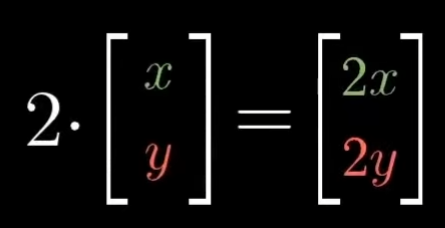
벡터와 선형 결합

 

1. 벡터의 조합

좌표상에 나타나는 벡터는 두 스케일된 벡터의 합으로 표현될 수 있습니다,

예) v와 w의 선형 결합은 av + bw 형태로 나타날 수 있으며 a와 b는 스칼라 값에 속합니다.

 

2. 선형 결합의 개념

모든 가능한 2차원 공간을 생각한다면 각 점은 특정 벡터 조합으로 표현됩니다. 개별 벡터를 화살표, 벡터의 전체 집합은 점으로 개념화합니다.

 

3. 선형 생성과 확장

선형 결합에 스케일된 세 번째 벡터를 더할 경우 기존에 생성된 공같의 바깥으로 나가지 않을 수도 있으며 무작위로 방향이 다른 세 번째 벡터를 선택한다면 새로운 차원의 방향을 포함하게 되며 모든 가능한 3차원 벡터를 생성할 수 있습니다.

 

4. 기저

기저는 벡터 공간을 생성하는 선형 독립 벡터들의 집합을 의미합니다. 

예) 2차원 공간의 기저 i = (1,0), j= (0,1)

 

이들은 2차원 평면의 모든 벡터를 표현할 수 있는 최소 집합입니다. 

 

벡터의 선형 결합은 다양한 차원 공간을 생성하며, 기저는 이 공간을 설명하는 최소 단위의 선형 독립 벡터 집합입니다. 차원이 확장될수록 더 많은 벡터와 방향을 포함합니다.