1번
int fun1(int n, int data[])
{
int sum = 0;
for (int i = 0; i < n; i += 2)
sum += data[i];
return sum;
}주어진 함수 fun1에서 반복문은 i가 0부터 시작하여 2씩 증가하면서 실행됩니다. 즉, i는 0, 2, 4, 6, ...과 같이 증가하며, 반복문이 실행되는 조건은 i < n입니다. 이로 인해 반복문은 n이 짝수일 때 약 n/2번, n이 홀수일 때 약 (n/2)번 실행됩니다.
따라서, 반복문은 대략 n/2번 실행되므로, 시간 복잡도는 O(n)입니다.
2번
int fun2(int m, int A[], int n, int B[], int C[])
{
int i = 0, j = 0, k = 0;
while (i < m && j < n)
{
if (A[i] < B[j])
C[k++] = A[i], i++;
else if (A[i] > B[j])
C[k++] = B[j], j++;
else
C[k++] = A[i], i++, j++;
}
while (i < m)
C[k++] = A[i], i++;
while (j < n)
C[k++] = B[j], j++;
return k;
}
첫 번째 while 루프
A[] 와 B[]를 비교하여 작은 값을 배열 c[]에 삽입하는 과정입니다. i와 j는 각각 A[] 와 B[]의 인덱스를 따라 증가합니다.
반복문은 최대 m+n번 반복합니다. 왜냐하면 i는 A[]의 길이 M만큼, j는 B[]의 길이 n만큼 증가하므로, 전체 반복 횟수는 m + n입니다.
따라서 이 루프의 시간 복잡도는 O(m+n)입니다.
두 번째 while 루프
첫 번째 while루프가 종료되면, i<m 또는 j<n 중 하나가 먼저 종료됩니다. 만약 a[]의 모든 원소가 먼저 c[]에 삽입되었다면, 남은 A[]의 원소들을 c[]에 복사해야 합니다. 최악의 경우 A[]의 모든 원소가 c[]에 복사될 수 있기 떄문에, 이 루프는 최대 O(m)번 반복됩니다.
세 번째 while 루프
만약 첫 번째 while 루프에서 A[]의 모든 원소가 먼저 c[]에 삽입되었다면, 이번에는 B[]의 남은 원소 c[]를 복사해야 합니다. 이 루프는 최악의 경우, B[]의 모든 원소를 c[]에 복사해야 하므로 최대 O(n)번 반복됩니다.
전체 시간 복잡도:
- 첫 번째 while 루프: O(m + n)
- 두 번째 while 루프: O(m) (최악의 경우)
- 세 번째 while 루프: O(n) (최악의 경우)
따라서 전체 시간 복잡도는 O(m + n)입니다.
3번
double fun3(int n)
{
double sum = 0;
for (double i = 1.0; i < n; i *= 1.5)
sum += i;
return sum;
}- i는 1.0에서 시작하여 매 반복마다 1.5배씩 증가합니다. 즉, i의 값은 1.0, 1.5, 2.25, 3.375, ...와 같이 커집니다.
- 루프는 i가 n에 도달하거나 이를 초과할 때 종료됩니다.
반복문 종료 조건:
반복문이 종료되는 시점은 i가 n 이상이 될 때입니다. i는 처음에 1에서 시작하여, 반복마다 1.5배씩 증가하므로 k번째 반복에서 i의 값은 i_k = 1.5^k입니다.
반복문이 종료되는 시점은 i_k >= n이므로:
이를 풀면 k에 대해 다음과 같은 식을 얻을 수 있습니다.
로그를 활용한 해결:
양변에 로그를 취해 k에 대한 식을 구할 수 있습니다. 로그를 취할 때 밑을 1.5로 두면:
하지만 로그의 밑을 바꾸면 다음과 같이 표현할 수 있습니다:
이는 k가 n에 대해 로그 속도로 증가함을 의미합니다.
따라서 반복문이 실행되는 횟수는 O(log n)이며, 이로 인해 해당 함수의 시간 복잡도는 O(log n)입니다
4번
int fun4(int n, int target, int data[])
{
int count = 0, i = 0, j = n - 1;
while (i < j)
{
if (data[i] + data[j] == target)
count++, i++, j--;
else if (data[i] + data[j] < target)
i++;
else
j--;
}
return count;
}이 함수는 두 숫자의 합이 주어진 target과 같은 쌍의 개수를 세는 함수입니다. 배열 data[]의 두 숫자의 합이 target과 같을 때, 해당 쌍을 하나로 카운트합니다.
while문 분석:
- i는 0부터 시작하고, j는 n-1부터 시작합니다.
- i와 j가 서로 교차하거나 같아질 때까지 반복문이 실행됩니다. 즉, i와 j가 만나는 시점에서 while문이 종료됩니다.
최악의 경우:
- i와 j가 반복문을 실행할 때마다 각각 한 칸씩 이동합니다. i는 증가하고, j는 감소합니다. 이때 i가 j와 만날 때까지 반복됩니다.
- 예를 들어, i = 0과 j = n-1로 시작하여, i는 1씩 증가하고, j는 1씩 감소하면서 i와 j가 만날 때까지 계속됩니다.
반복 횟수:
- i와 j가 하나씩 이동할 때마다 i와 j의 차이인 j - i가 1씩 줄어듭니다.
- 최악의 경우, i가 j에 도달할 때까지 반복이 진행되므로, 반복문은 최대 n-1번 실행됩니다.
결론:
따라서, 이 함수의 시간 복잡도는 O(n)입니다.
5번
int func5(int n, int K, int data[])
{
int count = 0;
for (int i = 0; i < n; i++)
{
int result = binary_search(n, data, K - data[i]);
if (result != -1)
count++;
}
return count;
}이 함수는 배열 data[]에서 두 숫자의 합이 K인 쌍의 개수를 세는 함수입니다. binary_search를 사용하여 각 data[i]에 대해 K - data[i]가 배열에 존재하는지 확인합니다.
시간 복잡도 분석:
1. for문:
- for문은 i가 0부터 n-1까지 반복됩니다. 따라서 최대 n번 반복되며, 이는 O(n)의 시간 복잡도를 가집니다.
2. 이진 검색:
- 각 반복에서 binary_search 함수가 실행됩니다. 이진 검색은 배열이 정렬되어 있을 때, K - data[i]의 값을 찾기 위해 배열을 절반씩 나누어 검색합니다.
- 이진 검색의 시간 복잡도는 O(log n)입니다. 이때 n은 배열의 크기를 나타냅니다.
3. 전체 시간 복잡도:
- for문은 n번 반복되고, 각 반복에서 이진 검색이 O(log n) 시간 복잡도를 가지므로, 전체 시간 복잡도는 O(n log n)입니다.
결론:
따라서 이 함수의 시간 복잡도는 O(n log n)입니다.
6번
int fun6(int m, int A[], int n, int B[])
{
for (int i = 0; i < m; i++)
{
for (int j = 1; j < n; j *= 2)
{
if (A[i] <= B[j])
break;
}
}
}이 함수는 두 배열 A[]와 B[]에 대해 특정 조건을 체크하는 과정입니다. 바깥쪽 for문은 A[]의 각 원소를 순차적으로 처리하고, 안쪽 for문은 B[] 배열의 인덱스를 1, 2, 4, 8, ...과 같이 2배씩 증가시켜가며 조건을 확인합니다.
시간 복잡도 분석:
1. 바깥 for문:
- 바깥 for문은 i가 0부터 m-1까지 반복됩니다. 따라서 바깥 for문은 최대 m번 반복되며, 이는 O(m)의 시간 복잡도를 가집니다.
2. 안쪽 for문:
- 안쪽 for문은 j가 1부터 시작하여, 매 반복마다 2배씩 증가합니다 (j *= 2). 이로 인해 j는 1, 2, 4, 8, 16, ...과 같은 값으로 증가하며, j가 n 이상이 될 때까지 반복됩니다.
- 이때, j가 2^k가 되어 2^k >= n일 때 종료되므로, 반복 횟수는 k번이며, 이는 (log n)입니다. 왜냐하면 k는 log_2 n에 비례하기 때문입니다.
3. 전체 시간 복잡도:
- 바깥 for문은 O(m)이고, 안쪽 for문은 O(log n)입니다.
- 따라서 전체 시간 복잡도는 O(m log n)입니다.
결론:
이 함수의 최악의 경우 시간 복잡도는 (m log n)입니다.
7번
int fun7(int n)
{
int count = 0;
for (int i = n; i > 0; i /= 2)
for (int j = 0; j < i; j++)
count += 1;
return count;
}이 함수는 두 개의 중첩된 반복문을 사용하고 있습니다. 바깥쪽 for문은 i가 n에서 시작하여 매 반복마다 절반씩 감소하고, 안쪽 for문은 j가 i까지 반복됩니다.
시간 복잡도 분석:
1. 바깥쪽 for문:
- 바깥쪽 for문에서 i는 매번 i /= 2로 절반씩 감소합니다. 즉, i의 값은 n, n/2, n/4, n/8, ...와 같이 감소하며, i가 1이 될 때까지 반복됩니다.
- 이 반복문은 약 log₂(n)번 실행되므로, O(log n)의 시간 복잡도를 가집니다.
2. 안쪽 for문:
- 안쪽 for문은 j가 0부터 i-1까지 반복됩니다. 즉, 각 반복에서 i번 반복이 수행됩니다.
- i의 값이 매번 절반씩 감소하므로, 안쪽 반복문에서 수행되는 연산 횟수는 n + n/2 + n/4 + ... + 입니다.
3. 등비수열의 합:
- 이 횟수는 등비수열의 합 형태를 따릅니다. 등비수열의 합 공식에 따르면,
즉, 전체 실행 횟수는 대략 2n번에 해당합니다.n + n/2 + n/4 + n/8 + ... + 1 ≈ 2na/1-r
결론:
따라서 이 함수의 시간 복잡도는 O(n)입니다.
| 자료구조 | Push/Enqueue | Pop/Dequeue | |
| 스택 | 배열 | 배열의 마지막에 삽입 → O(1) | 배열의 마지막 요소를 제거 → O(1) |
| 단방향 연결리스트 | 새로운 노드를 맨 앞에 추가 → O(1) | 맨 앞 노드를 제거하고 head를 다음 노드로 이동 → O(1) | |
| FIFO 큐 | 원형 배열 | rear(마지막) 위치에 삽입 → O(1) | front(앞) 위치에서 제거 → O(1) |
| 단방향 연결리스트 | tail에서 삽입 → O(1) | head(앞)에서 제거 → O(1) | |
1. 스택(Stack)
스택은 후입선출(LIFO: Last In, First Out) 방식으로 동작하는 자료구조입니다. 마지막에 들어간 데이터가 먼저 나오는 구조입니다.
배열을 이용한 스택
- Push (삽입): 배열의 마지막에 새로운 요소를 삽입합니다. 배열에서 마지막 위치에 데이터를 추가하는 것은 O(1)의 시간복잡도를 가집니다.
- Pop (제거): 배열에서 마지막 요소를 제거합니다. 마지막 요소를 삭제하는 작업은 O(1)의 시간복잡도로 처리할 수 있습니다.
단방향 연결리스트를 이용한 스택
- Push (삽입): 새로운 노드를 맨 앞에 추가합니다. 연결리스트에서는 새로운 노드를 추가할 때, 단지 head 포인터를 새 노드로 이동시키면 되므로 O(1)입니다.
- Pop (제거): head를 다음 노드로 변경합니다. 즉, 첫 번째 노드를 제거하는 방식이므로 O(1)입니다.
2. FIFO 큐 (First In, First Out)
큐는 선입선출(FIFO: First In, First Out) 방식으로 동작합니다. 가장 먼저 들어간 데이터가 가장 먼저 나옵니다.
원형 배열을 이용한 큐
- Enqueue (삽입): 큐의 rear(뒤쪽) 위치에 새 데이터를 삽입합니다. 원형 배열에서는 rear가 배열의 끝에 도달하면 다시 처음으로 돌아가므로, 삽입은 O(1)입니다.
- Dequeue (제거): 큐의 front(앞쪽) 위치에서 데이터를 제거합니다. 큐에서 앞쪽을 제거하는 것도 O(1)입니다.
단방향 연결리스트를 이용한 큐
- Enqueue (삽입): 큐의 tail(뒤쪽)에서 새 데이터를 삽입합니다. 연결리스트에서는 tail 포인터를 사용하여 데이터를 추가하는데, 이는 O(1)입니다.
- Dequeue (제거): 큐의 head(앞쪽)에서 데이터를 제거합니다. head를 단순히 다음 노드로 갱신하는 작업은 O(1)입니다.
정리
- 스택 (Stack):
- 배열에서는 삽입과 제거가 O(1)로 빠르게 처리됩니다.
- 단방향 연결리스트에서는 Push는 O(1), Pop도 O(1)로 효율적입니다.
- 큐 (Queue):
- 원형 배열에서는 삽입과 제거가 각각 O(1)로 빠르게 처리됩니다.
- 단방향 연결리스트에서는 Enqueue와 Dequeue가 모두 O(1)입니다.
이 자료구조들은 모두 연산에 대해 O(1)의 시간복잡도를 가지므로, 빠르게 데이터를 삽입하고 삭제할 수 있는 특징이 있습니다.
| 자료구조 | 검색 | 삽입 | 삭제 | |
| 배열 | 정렬안함 | 최악의 경우 찾으려는 원소가 마지막에 위치함 하나씩 비교하면 O(n) | 최악의 경우 첫번째 위치에 삽입하면 뒤의 원소들을 모두 한칸씩 이동해야함 n개의 원소를 이동하기 때문에 O(n) | 최악의 경우 첫번째 원소 삭제하면 뒤의 원소들을 모두 한칸씩 앞으로 이동해야함 n개의 원소를 이동하기 때문에 O(n) |
| 오름차순으로 정렬함 | 이진탐색을 통해 검색을 하면 O(log n) | 이진탐색을 통해 삽입할 위치를 찾는 시간복잡도는 O(log n)이고 삽입할 시 최악의 경우는 첫번째 위치에 삽입하면 모든 원소를 뒤로 이동해야하므로 시간복잡도는 O(n)임 따라서 최악의 경우 시간복잡도는 O(n) |
삽입과 마찬가지로 삭제할 위치를 찾는 시간복잡도는 O(log n), 최악의 경우 첫번째 원소를 삭제하면 모든 원소를 앞으로 이동해야하므로 시간복잡도는 O(n) 즉 삭제의 최악의 시간복잡도는 O(n) | |
| 연결 리스트 |
정렬안함 | 최악의 경우 찾으려는 원소가 마지막에 위치함 첫 노드부터 하나씩 비교하면 O(n) | 원하는 위치에 새로운 노드를 추가하는 것으로 삽입 위차만 알면 포인터를 이용해 새 노드를 추가할 수 있는데 정렬되지 않은 상태이므로 뒤에 추가하면 새로운 노드를 마지막이 가리키는 곳에 삽입 즉 현재 노드의 포인트만 수정하면 되므로 O(1) | 삭제할 노드 찾는 시간은 O(n)이지만 고려하지 않는다고 했으므로 삭제할 노드의 이전 노드가 삭제할 다음 노드를 가리키도록 수정하면 쉽게 삭제 되므로 O(1) |
| 오름차순으로 정렬함 | 최악의 경우 찾으려는 원소가 마지막 노드에 위치하면 첫노드부터 순차적으로 비교하며 진행해야하므로 O(n) |
새로운 노드를 삽입하는 것은 O(1)이지만 삽입 위치를 찾는 과정이 O(n) 즉 전체적으로 O(n) | 삭제할 노드의 위치를 찾는데 O(n)이 걸리지만 삭제할 위치를 찾는 시간은 제외한다고 했으므로 O(1) | |
1. 배열 (Array)
정렬 안 함
- 검색 (찾기): 배열이 정렬되지 않았을 경우, 원하는 원소를 찾기 위해 모든 원소를 비교해야 합니다. 최악의 경우는 찾으려는 원소가 배열의 마지막에 있을 수 있으므로 O(n) 시간이 걸립니다.
- 삽입: 배열에서 삽입할 위치를 찾는 시간은 O(1)이지만, 삽입 후 배열의 크기를 한 칸씩 밀어야 하므로 최악의 경우 첫 번째 자리에 삽입하려면 나머지 모든 원소를 한 칸씩 뒤로 밀어야 합니다. 이로 인해 O(n) 시간이 걸립니다.
- 삭제: 배열에서 삭제할 때도 마찬가지로 O(1)로 삭제할 위치를 찾을 수 있지만, 삭제 후 나머지 원소들을 한 칸씩 앞으로 밀어야 하므로 최악의 경우 O(n) 시간이 걸립니다.
정렬된 배열
- 검색 (이진 탐색): 배열이 정렬되어 있을 경우, 이진 탐색을 통해 원소를 찾을 수 있습니다. 이진 탐색의 시간 복잡도는 O(log n)입니다.
- 삽입: 삽입할 위치를 찾기 위해 이진 탐색을 사용하면 O(log n) 시간이 걸리지만, 최악의 경우에는 첫 번째 위치에 삽입해야 하므로 나머지 원소를 뒤로 이동시켜야 하고, 이로 인해 O(n) 시간이 걸립니다. 따라서 전체 시간 복잡도는 O(n)입니다.
- 삭제: 삭제할 위치를 찾기 위해 이진 탐색을 사용하면 O(log n) 시간이 걸리지만, 첫 번째 원소 삭제 시 나머지 원소들을 한 칸씩 앞으로 이동시켜야 하므로 O(n) 시간이 걸립니다. 따라서 삭제의 최악 시간 복잡도는 O(n)입니다.
2. 연결리스트 (Linked List)
정렬 안 함
- 검색 (찾기): 연결리스트에서 원소를 찾으려면 첫 번째 노드부터 하나씩 순차적으로 비교해야 하므로 O(n) 시간이 걸립니다.
- 삽입: 연결리스트에서 새로운 노드를 삽입할 때는 위치를 알면 O(1)로 빠르게 삽입할 수 있습니다. 예를 들어, 뒤에 추가하면 tail 포인터만 수정하면 되므로 O(1)입니다.
- 삭제: 삭제할 노드를 찾는 시간은 O(n)입니다. 그러나 삭제할 위치를 찾은 후 O(1)로 노드의 포인터를 수정하면 삭제가 가능합니다. 따라서 삭제는 O(1)이 걸립니다.
정렬된 연결리스트
- 검색 (찾기): 정렬된 연결리스트에서 원소를 찾는 것은 순차 탐색이므로 최악의 경우 O(n) 시간이 걸립니다.
- 삽입: 삽입할 위치를 찾는 데 O(n) 시간이 걸리고, 삽입은 O(1)이므로 전체 시간 복잡도는 O(n)입니다.
- 삭제: 삭제할 위치를 찾는 데 O(n) 시간이 걸리며, 삭제는 O(1)입니다.
정리
- 배열:
- 정렬 안 함:
- 검색: O(n), 삽입: O(n), 삭제: O(n)
- 정렬됨:
- 검색: O(log n) (이진 탐색), 삽입: O(n), 삭제: O(n)
- 정렬 안 함:
- 연결리스트:
- 정렬 안 함:
- 검색: O(n), 삽입: O(1), 삭제: O(1)
- 정렬됨:
- 검색: O(n), 삽입: O(n), 삭제: O(1)
- 정렬 안 함:
핵심 포인트:
- 배열에서는 삽입과 삭제가 O(n) 시간이 걸릴 수 있습니다.
- 연결리스트에서는 삽입과 삭제가 O(1)로 처리되지만, 검색은 O(n)이 걸립니다.
4번
1. 15^10 n + 12099
- 이 식을 보면 n에 비례하는 항과 상수항이 있습니다.
- 최고차항인 15^10 * n에서 15^10은 상수이므로, n에 대한 시간 복잡도는 O(n)으로 간주됩니다.
- 상수항과 최고차항의 계수는 Big-O 표기법에서 무시되므로 O(n)입니다.
- 결론: O(n), 따라서 O(n^2)에는 포함되지 않습니다.
2. n^1.98
- 이 식은 n의 1.98제곱입니다. 따라서 시간 복잡도는 O(n^1.98)입니다.
- n^2보다 작지만, 이 역시 O(n^2)의 상한선에 포함됩니다. 왜냐하면 O(n^1.98)는 O(n^2)보다 더 빠르게 증가하지 않으므로, O(n^2)으로도 표현 가능합니다.
- 결론: O(n^2)에 포함됩니다.
3. n^3 / sqrt(n)
- 이 식은 n^3 / sqrt(n)입니다. 이를 정리하면 n^2.5입니다.
- O(n^2.5)는 O(n^2)보다 빠르게 증가합니다. n^2보다 큰 시간 복잡도 함수는 O(n^2)에 포함되지 않습니다.
- 결론: O(n^2)에는 포함되지 않습니다.
4. 2^20 * n
- 이 식에서 2^20은 상수이고, n은 변수입니다. 따라서 이 식의 시간 복잡도는 O(n)입니다.
- O(n)은 O(n^2)보다 작지만, 여전히 O(n^2)에 포함될 수 있습니다. 왜냐하면 O(n^2)는 O(n)을 포함하는 상한선이기 때문입니다.
- 결론: O(n), 따라서 O(n^2)에 포함됩니다.
결론
- O(n^2)에 포함되지 않는 것은 (3) n^3 / sqrt(n) (O(n^2.5))입니다. 이 식은 O(n^2)보다 빠르게 증가하므로 포함되지 않습니다.
5번
다음 4가지 함수를 점근적 차수가 낮은 것부터 높은 것 순으로 나열
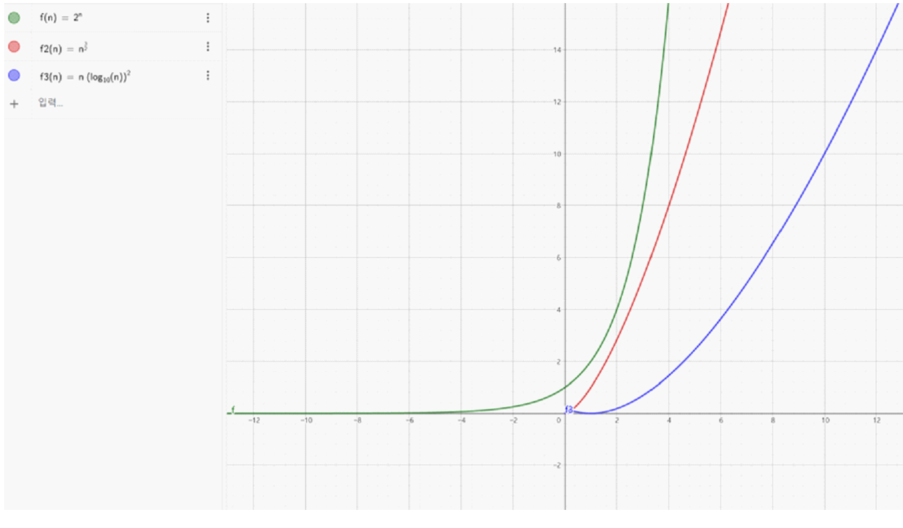
함수의 점근적 차수에서, 로그 함수는 다항 함수보다 느리게 증가하고, 지수 함수는 다항 함수보다 빠르게 증가합니다. 순으로 f_3 < f_2 < f_1나열됨
6번

7번

'IT 프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 그룹액티비티2 (0) | 2025.03.23 |
|---|---|
| [알고리즘] 멱집합 (0) | 2025.03.20 |
| [알고리즘] 이진 검색과 정렬 (0) | 2025.03.15 |
| [알고리즘의 분석] 시간복잡도 (0) | 2025.03.14 |
| [알고리즘] maze (0) | 2025.03.14 |