P(n,r) = n(n-1)(n-2)...(n-r+1) r <= n
예시
100명이 참여한 경품에서 1등, 2등, 3등을 한 명씩 선발하는 방법은 모두 몇 가지 인가?
P(100,3) = 970,200 가지입니다.
P(10, 4) = 10 * 9 * 8 * 7 = 5040
조합 (Combinations)
n개의 다른 원소로 구성된 집합이 있습니다. r-조합은 r개 원소에 대한 unordered selection입니다. r <= n 입니다.
r 조합의 개수는 다음과 같이 표기할 수 있습니다 .C(n,r)

대각선을 그었을 때 대각선 위로 이동하지 않는 개수는 어떻게 될까요?
- Gn + Bn = C(2n, n)
좋은 경로의 개수는 나쁜 경로를 빼주면 되는데요.
Bad route의 개수는 (n+1) * (n-1) grid가 되는데요.
이는 나쁜 경로가 하나 주어졌다고 봅니다. 이 나쁜 경로를 변경시킵니다. 대각선을 벗어나는 첫 번째 이동을 찾고 그것을 반전시키는 것입니다. 이 나쁜 경로를 변형하면 ( n - 1 ) ( n + 1 ) 의 경로가 나타납니다.

함수는 1:1 함수가 됩니다.

좋은 경로의 개수는 C(2n, n) - Bn 이므로 이는
C(2n, n) - C(2n, n-1) = c(2n,n) / n + 1
이를 카탈랑 수라고 합니다.

이항계수
a+b 를 전개한다고 가정할 때 이는 (a+b)^n = (a+b)(a+b) ... (a+b) 입니다.
1. 각각의 factor에서 a와 b를 선택합니다.
2. 이것을 서로 곱하고
3. 전개된 것을 모두 더하면 값이 나옵니다.
a^n-k * b^k 가 어떻게 나타내는지 파악을 하고 n-k 는 a를 선택한다고 가정을 합니다.

a^n-k b^k 는 C(n.k ) 번 나타납니다.

이항정리에 의해서

(x + y + z ) ^ 9 = (x+y+z) (x+y+z) ... (x+y+z) (9 terms)
여기서
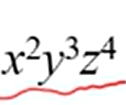
이것을 구하고 싶을 때는
-x chosen from 2 of the 9 terms.
-y chosen from 3 of the 7 terms
-z chosen from 4 of the 4 terms
을 통해서
C(9, 2) C(7, 3) = 36 * 35 = 1260이 나오게 됩니다.
'IT 프로그래밍 > 이산수학' 카테고리의 다른 글
| 베이즈정리 (0) | 2024.06.12 |
|---|---|
| 순열의 조합 (0) | 2024.06.11 |
| 경우의 수 확률 세기 (0) | 2024.06.11 |
| [이산수학] 재귀적 알고리즘 (0) | 2024.06.11 |
| [이산수학] 함수의 증가, big o notation (0) | 2024.04.13 |