스패닝트리
그래프 G가 주어졌을 때 트리 T는 그래프 G는 신장 트리입니다.
- T가 그래프 G의 서브그래프이고
- T가 G의 모든 정점을 포함할 때
이런 경우 스패닝 트리라고 합니다. 그래프의 모든 정점을 포함하는 트리라고 보면 됩니다.

최소스패닝트리
가중치 그래프 G가 주어졌을 때 제일 첫 번째 단계에서는 시작 정점을 하나 선택을 합니다. 우리가 찾으려고 하는 스패닝트리에 이 시작 정점이 추가됩니다.
Kruskal's algorithm
이 간선이 1의 가중치를 가지기 때문에 선택이 됩니다. 나머지 간선들 중에 역시 가장 작은 간선이 계속적으로 선택이 되고 싸이클을 생성하지 않는 간선을 계속적으로 선택해나가면 됩니다.
Binary trees
이진트리
이진트리는 각각의 정점이 0개 또는 1개 또는 2개의 자식을 가지는 루트트리
완전이진트리
각 정점이 가지는 것이 2개 아니면 0개인 것을 말합니다. 정점들이 가지는 자식의 수를 보면 0개 아니면 2개인 것입니다.
완전이진트리
T는 i+1의 terminal vertices를 가지고 2i+1의 total number of vertice를 가집니다.

만약 t = 2^h 가 성립하는 경우는 어떤 경우일까요?
완전 이진트리 t에서 모두 다 같은 레벨의 트리 t를 가진다면 단말정점의 개수는 2^h가 됩니다.

이진 탐색 트리
최악의 경우 비교 횟수는 트리의 높이에 비례
최선은 먼저 오른차순으로 정렬을 시키고 가운데 문자열을 루트로 정하고 반반을 나눠 왼쪽과 오른쪽으로 나누면 됩니다. 그리고 계속 가운데 값을 배치시키면 됩니다.
트리운행
트리의 각 정점을 한번씩 방문하는 순서를 정하는 것입니다. 첫번째는
전위 운행법
이진트리에서 정점을 방문하는 순서로 Root를 먼저 가고 그 다음 Left 그 다음 Right를 가면 됩니다. 처음 루트를 방문하고 left를 먼저 돈 다음 이후 right를 가면 됩니다.

후위 운행법
Left-Right-Root 순서입니다. 따라서 root를 기준으로 왼쪽편을 먼저 가고 이후 오른쪽을 돈 다음에 마지막에 root를 갑니다.

중위 운행법
Left-Root-Right 순서입니다. Root의 왼쪽편이 방문되었다 하고 이후 Root 이후 Right순으로 합니다.

아래와 같은 그림처럼 수식을 구해줄 수 있습니다.
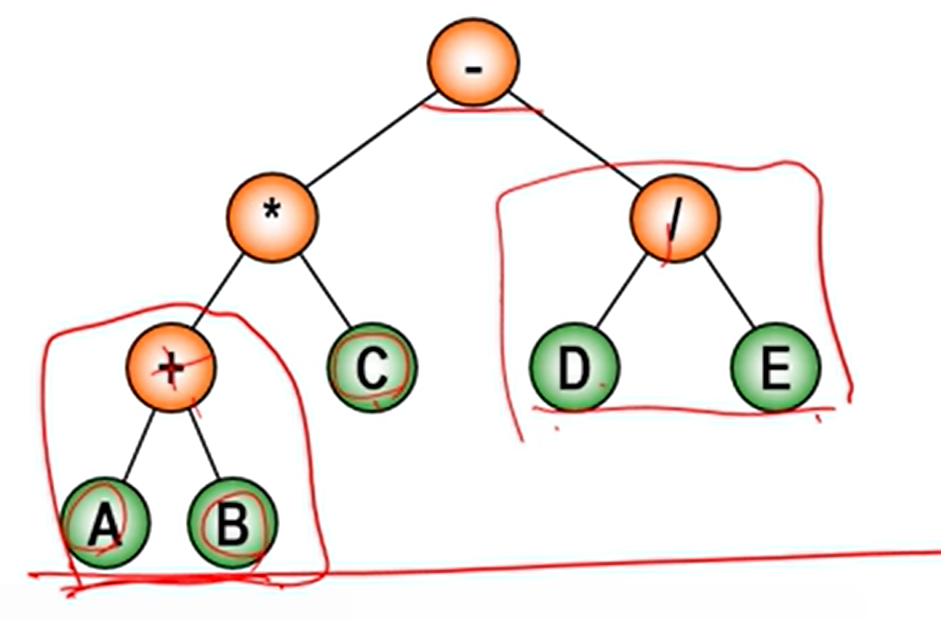
결정트리
결정트리는 어떤 행동을 할 것인지를 알고리즘을 포함하는 이진트리를 결정트리라고 합니다. 결정트리는 알고리즘을 명시하기 위해서 사용하거나 worst-case의 lower bound를 결정할 때 사용합니다.
어느 식당에 갈 것인지를 결정해야 하는데 이에 대한 것을 트리 형태로 사용할 수 있습니다.
정렬 알고리즘의 최악의 경우 f(n) = n log n 의 복잡도를 가집니다.

이진트리의 동형
- 루트트리의 동형 관계를 만족
- T1에서의 왼쪽(오른쪽) 자식이 T2에서의 왼쪽(오른쪽)자식이 되어야 한다.
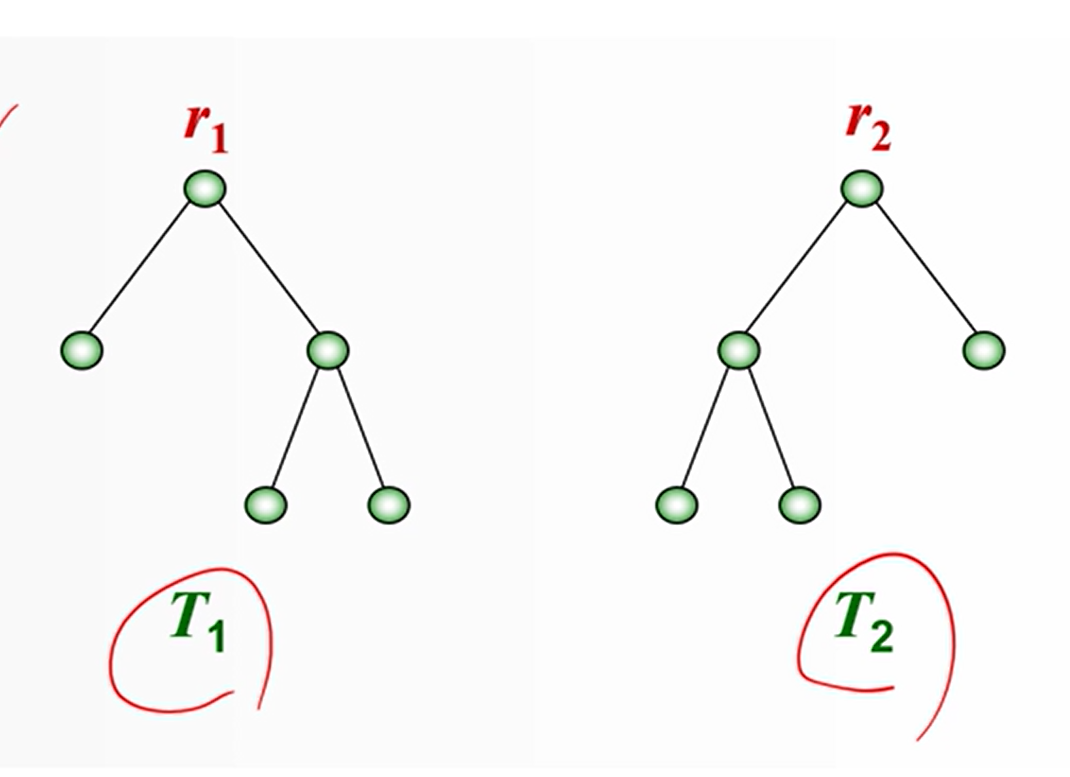
루트트리로서는 동형이 성립합니다.
하지만 이것을 왼쪽과 오른쪽을 기준으로 볼 때는 동형이 아니기 때문에 이진트리에서는 동형이 아닙니다.
'IT 프로그래밍 > 이산수학' 카테고리의 다른 글
| 차별성함수 (0) | 2024.06.18 |
|---|---|
| [이산수학] 그래프 간선 정점 완전 차수 오일러 싸이클 동형 (0) | 2024.06.12 |
| 이진 탐색 알고리즘 (0) | 2024.06.12 |
| 베이즈정리 (0) | 2024.06.12 |
| 순열의 조합 (0) | 2024.06.11 |