힙 정렬(Heap Sort) 개요
최악의 경우 시간 복잡도:
- O(nlogn)
특징:
- 제자리 정렬(Sort in Place): 추가 배열이 필요하지 않음
- 이진 힙(Binary Heap) 구조 사용
힙(Heap)
힙은 완전 이진 트리(Complete Binary Tree) 이면서 힙 속성(Heap Property) 을 만족해야 합니다.
- 완전 이진 트리(Complete Binary Tree):
- 마지막 레벨을 제외하면 모든 레벨이 완전히 채워져 있어야 합니다.
- 마지막 레벨에서는 왼쪽부터 연속된 노드만 존재할 수 있습니다.
힙 속성(Heap Property)
- 최대 힙(Max Heap) 속성:
- 부모 노드는 자식 노드보다 크거나 같아야 합니다.
- 최소 힙(Min Heap) 속성:
- 부모 노드는 자식 노드보다 작거나 같아야 합니다.
이번 정렬에서는 최대 힙(Max Heap) 을 다룹니다.
힙은 일차원 배열로 표현 가능
A[1...n]
- 루트 노드 A[1].
- A[i]의 부모 = A[i/2]
- A[i]의 왼쪽 자식 = A[2i]
- A[i]의 오른쪽 자식 = A[2I+1]
MAX-HEAPIFY
HEAPIFY 연산
HEAPIFY는 힙 속성을 만족하지 않는 루트 노드 하나만을 조정하여 전체 트리를 힙으로 변환하는 연산입니다.
HEAPIFY의 전제 조건
- 완전 이진 트리(Complete Binary Tree) 여야 합니다.
- 루트 노드를 제외한 왼쪽 서브트리와 오른쪽 서브트리는 이미 각각 힙을 이루고 있어야 합니다.
- 유일하게 루트 노드만이 힙 속성을 만족하지 않는 상태에서 시작합니다.
이 상황에서 HEAPIFY는 루트 노드를 아래로 내려서 힙 속성을 만족하도록 조정합니다.
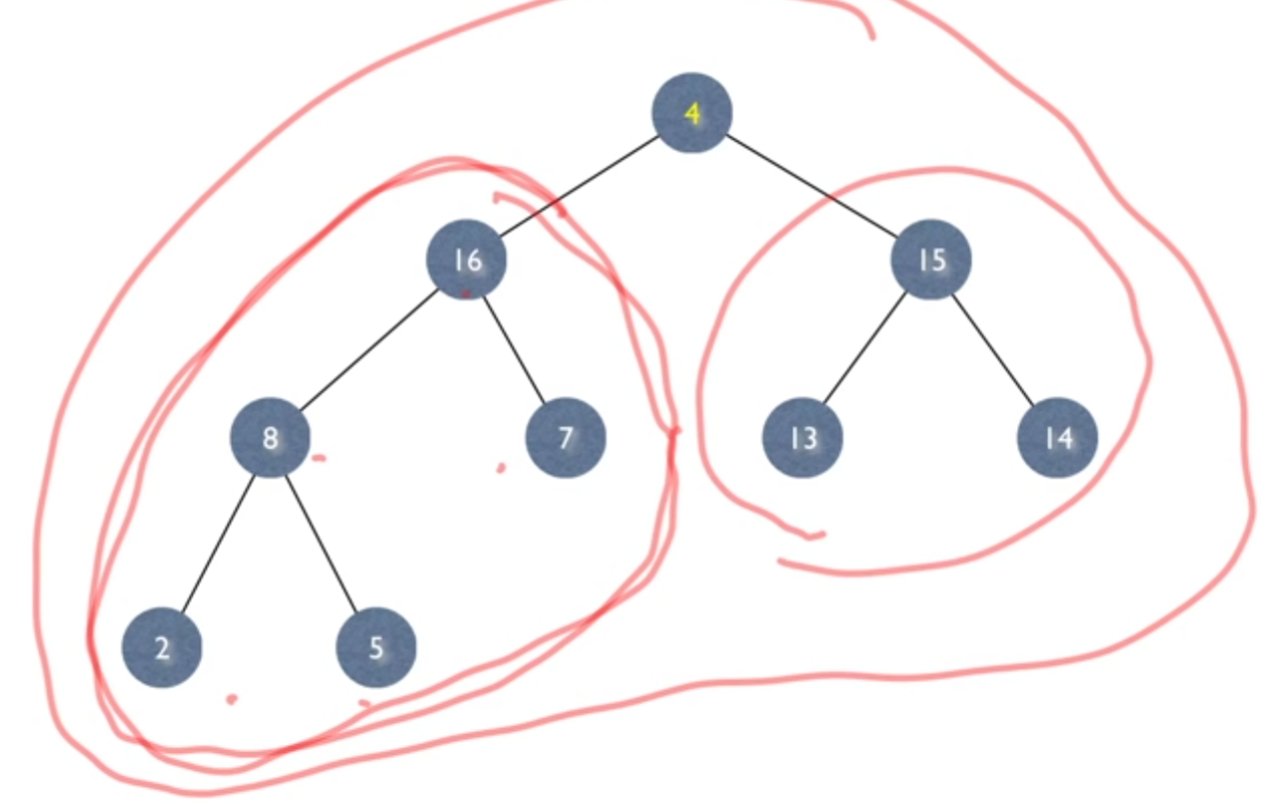
HEAPIFY 과정
- 루트 노드의 두 자식 중 더 큰 값을 가진 노드를 선택합니다.
- 만약 루트 노드의 값이 그보다 작다면 둘의 위치를 교환합니다.
- 교환된 자리를 새로운 루트로 삼고 재귀적으로 같은 과정을 반복합니다.
- 더 이상 교환이 필요 없거나 리프 노드에 도달하면 종료됩니다.
예제
- 루트 노드가 4, 왼쪽 자식이 16, 오른쪽 자식이 15라면 16이 더 크므로 16과 4를 교환합니다.
- 이후 4의 새로운 위치에서 같은 과정을 반복하여 힙 속성을 만족하도록 합니다.
MAX-HEAPIFY(A, i)
{
if there is no child of A[i]
return;
k < -index of the biggest child of i;
if A[i] >= A[k]
return;
exchange A[i] and A[k];
MAX - HEAPIFY(A, k);
}설명:
- 자식이 없다면 종료
- 더 큰 자식을 찾아 k에 저장
- 루트가 더 크면 종료, 아니라면 자리 교환 후 재귀적으로 HEAPIFY 실행
MAX-HEAPIFY(A, i)
{
while A[i] has a child do
k <-index of the biggest child of i;
if A[i] >= A[k]
return;
exchange A[i] and A[k];
i =k
end
}설명:
- 재귀 없이 반복문을 사용하여 while 루프로 처리
- 힙 속성을 만족할 때까지 교환 반복
- 리프 노드에 도달하거나 교환이 필요 없을 때 종료
'IT 프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 이진 검색 트리 (0) | 2025.04.07 |
|---|---|
| 트리 (0) | 2025.04.07 |
| [알고리즘] mergesort (0) | 2025.03.27 |
| [알고리즘] 정렬 (0) | 2025.03.27 |
| [알고리즘] 그룹액티비티2 (0) | 2025.03.23 |