- 여러 개의 키 저장
- INSERT, SEARCH, DELETE
여러 개의 키를 저장하고 검색, 삽입, 삭제 작업을 효율적으로 수행하기 위해 다양한 자료구조가 사용됩니다. 아래는 배열과 연결 리스트를 사용할 경우, 정렬 여부에 따른 시간 복잡도를 정리한 표입니다:
| 자료구조 | 정렬여부 | Search | Insert | Delete |
| 배열 (Array) | 정렬됨 | O(log n) | O(n) | O(n) |
| 배열 (Array) | 정렬되지 않음 | O(n) | O(1), O(n) | O(1) |
| 연결 리스트 (Linked List) | 정렬됨 | O(n) | O(n) | O(1) |
| 연결 리스트 (Linked List) | 정렬되지 않음 | O(n) | O(1) | O(1) |
- 🔍 배열이나 연결 리스트를 사용하는 경우, 정렬 여부와 상관없이 INSERT, SEARCH, DELETE 중 적어도 하나는 O(n)의 시간 복잡도를 가집니다.
이와 같은 트리 기반 자료구조는 균형 유지 알고리즘을 통해 평균 및 최악의 경우에도 효율적인 연산이 가능합니다.
또한,
- 직접 주소 테이블 (Direct Address Table)
- 해시 테이블 (Hash Table)
등의 해싱 기반 자료구조는 적절한 해시 함수와 충돌 해결 기법을 사용하면 **삽입, 검색, 삭제 모두 평균적으로 O(1)**의 성능을 기대할 수 있습니다.
검색트리
검색 트리는 동적 집합 을 트리 구조로 구현한 것입니다.
이 구조에서는 검색(Search), 삽입(Insert), 삭제(Delete) 연산이 트리의 높이에 비례하는 시간 복잡도를 가집니다.
대표적인 검색 트리에는 다음과 같은 종류가 있습니다:
- 이진 검색 트리 (Binary Search Tree, BST)
- 레드-블랙 트리 (Red-Black Tree)
- B-트리 (B-Tree) 등
이진검색트리
이진 검색 트리는 이진 트리의 일종으로, 각 노드에 하나의 키가 저장되며 다음과 같은 조건을 만족합니다:
- 어떤 노드 v에 대해:
- 왼쪽 서브트리의 키 ≤ key[v]
- 오른쪽 서브트리의 키 ≥ key[v]
즉, 왼쪽은 작거나 같고, 오른쪽은 크거나 같다는 성질이 있어, 트리를 따라 내려가며 이진 탐색을 할 수 있습니다.

이진트리의 각 노드에 하나의 키가 저장되어 있으면서 오른쪽에 있는 것은 크거나 같은 것을 볼 수 있습니다. 왼쪽에 있는 것은 같거나 같은 것을 볼 수 있습니다.
TREE-SEARCH(x, k)
if x = NIL or k = key[x]
then return x
if k < key[x]
then return TREE-SEARCH(left[x], k)
else return TREE-SEARCH(right[x], k)
Iterative Version -SEARCH
ITERATIVE-TREE-SEARCH(x, k)
while x != NULL and k != key[x]
do if k < key[x]
then x <- left[x]
else x <- right[x]
return x두 알고리즘 모두 시간복잡도는 O(h)입니다.
트리 높이에 따른 시간복잡도 예시
- 균형잡힌 이진 트리의 경우:
→ 높이 h = O(log n) → 탐색 시간도 O(log n) - 편향된 트리(선형 구조)의 경우:
→ 높이 h = O(n) → 탐색 시간도 O(n) (최악의 경우)
따라서, 트리의 균형을 유지하는 것이 효율적인 연산을 위한 핵심입니다.
이런 이유로 AVL 트리, 레드-블랙 트리와 같은 **균형 이진 탐색 트리(Balanced BST)**가 자주 사용됩니다.
최소값
어떤 노드가 최소값이 되기 위해서는:
- 왼쪽 자식이 없어야 하며,
- 다른 노드의 오른쪽 서브트리에 속하면 안 됩니다.
(오른쪽 서브트리에 있다는 것은 해당 노드보다 크다는 의미이기 때문입니다.)
개념
- 최소값은 항상 루트에서 시작해 왼쪽 자식 노드만 따라가다 더 이상 내려갈 수 없는 노드입니다.
- 따라서 가장 왼쪽 노드가 트리에서 가장 작은 값을 가집니다.
TREE-MINIMUM(x)
while left[x] != NIL
do x <- left[x]
return x최소값은 항상 가장 왼쪽 노드에 존재
시간복잡도 : O(h)
최대값
TREE-MAXIMUM(x)
while right[x] != NIL
do x <- right[x]
return x최대값은 최소값의 반대 개념으로,
오른쪽 자식만 따라가다 더 이상 내려갈 수 없는 노드가 트리에서 가장 큰 값을 가집니다.
시간복잡도 : O(h)
Successor
정의
어떤 노드 x의 Successor(후속 노드)란,
key[x]보다 크면서 가장 작은 키를 가진 노드를 의미합니다.
즉, x보다 바로 다음으로 큰 값을 가진 노드입니다.
(단, 모든 키는 서로 다르다고 가정)
3가지 경우
- 노드 x의 오른쪽 부트리가 존재할 경우, 오른쪽 부트리의 최소값
- 오른쪽 부트리가 없는 경우, 어떤 노드 y의 왼쪽 부트리의 최대값이 x가 되는 그런노드 y가 x의 successor (부모를 따라 루트까지 올라가면서 처음으로 누군가의 왼쪽 자식이 되는 노드)
- 그런 노드 y가 존재하지 않을 경우 successor가 존재하지 않음
TREE-SUCCESSOR(x)
if right[x] != NIL
then return TREE-MINUMUM(right[x])
y <- p[x]
while y != NIL and x = right[y]
do x <- y
y <- p[y]
return y시간복잡도 : O(h)
Presuccessor는 반대로 하면 됩니다. 이 경우에도 시간복잡도는 successor와 같습니다.
INSERT
개념
이진 검색 트리에서 INSERT는 새로운 노드를 트리에 추가하는 연산입니다.
기존 노드의 위치는 변경하지 않으며, 삽입 위치는 항상 leaf 자리로 찾아 내려갑니다.
삽입 방식 요약
- 새로운 키를 삽입할 때는 검색할 때처럼 크기를 비교하며 트리를 따라 내려갑니다.
- 삽입할 위치는 더 이상 자식이 없는 leaf 자리, 즉 NIL이 되는 위치입니다.
- 삽입 과정에서 기존의 트리 구조는 전혀 손상되지 않으며, 새로운 노드만 연결됩니다
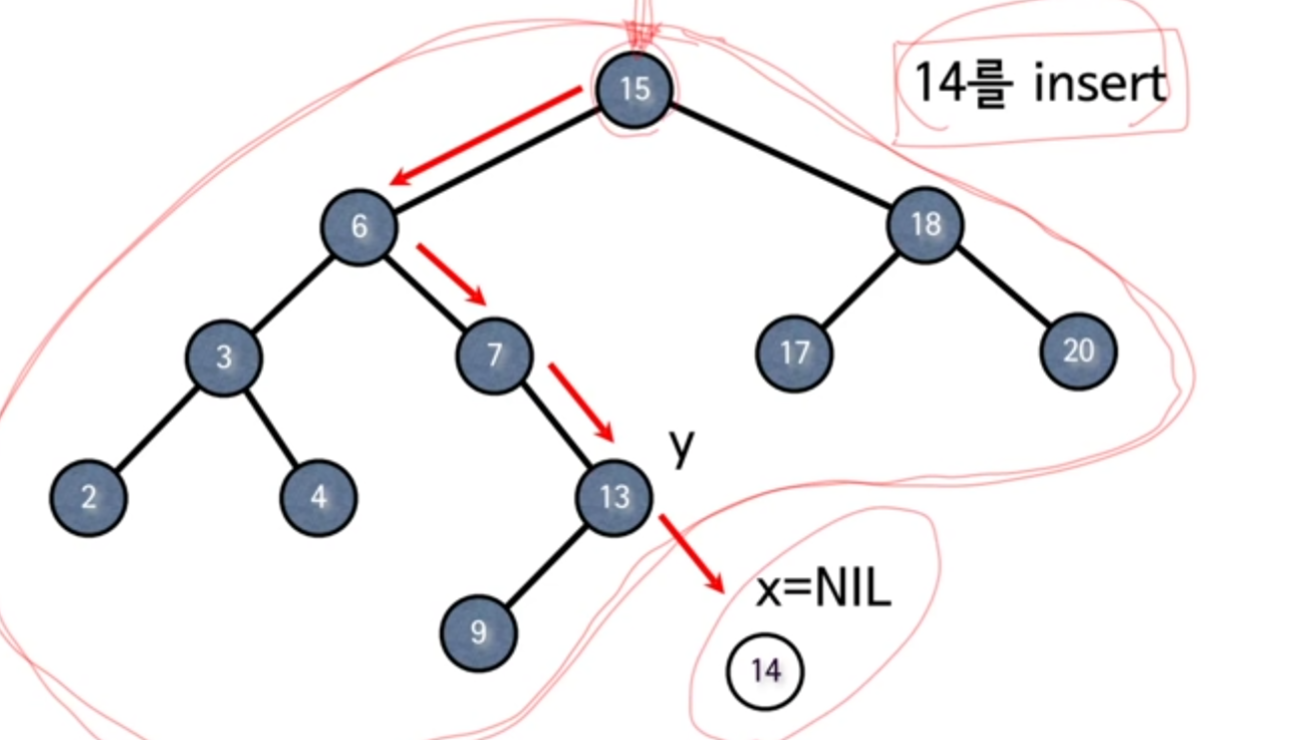
예시 설명
예를 들어, 14를 삽입하려고 할 때:
- 루트 15보다 작으므로 왼쪽으로
- 6보다 크므로 오른쪽으로
- 7, 13보다 크므로 계속 오른쪽으로 내려갑니다
- 13의 오른쪽 자식이 비어 있다면, 그 자리에 14를 삽입합니다.
구현 아이디어
삽입 위치를 추적하기 위해 두 개의 포인터를 사용합니다:
- x: 트리에서 내려가며 비교하는 포인터
- y: x의 부모 노드를 기억 (삽입할 위치의 부모가 됨)
x가 NIL이 되는 순간, y는 삽입할 위치의 부모 노드를 가리킵니다.
그 위치에 새 노드 z를 연결하면 됩니다.

맨 처음에 empty binary tree에 6개의 key를 삽입해서 binary를 나타낸 것입니다. 첫번째 30을 insert하면 30이 되고 20이 insert되면 b처럼 되고 25, 40, 10, 그리고 35를 전부 다 배치하면 f처럼 됩니다.
binary search tree가 자라는 방식입니다. 따라서 delete하지 않는다면 계속 차지하는 구조입니다.
TREE-INSERT(T,z)
y -> NIL
X <- root[T]
while x != NIL
do y <- x
if key[z] < key[x]
then x <- left[x]
else x <- right[x]
p[z] <- y
if y = NIL
then root[T] <- z
else if key[z] < key[y]
then left[y] <- z
else right[y] <- z시간복잡도 : O(h)
DELETE
DELETE: 이진 검색 트리에서의 삭제
이진 검색 트리에서 DELETE 연산은 특정 키 값을 갖는 노드를 트리에서 제거하는 작업입니다.
우선 SEARCH 연산을 통해 삭제할 노드를 찾고, 그 위치에서 삭제 연산을 수행합니다.
삭제 경우의 분류
삭제는 노드의 자식 수에 따라 다음 세 가지 경우로 나뉩니다:
Case 1. 자식이 없는 경우 (Leaf Node)
- 단순히 해당 노드를 트리에서 제거하면 됩니다.
- 부모 노드가 가리키던 포인터를 NULL로 바꿔주면 됩니다

Case 2. 자식이 하나인 경우
- 삭제 노드의 자식 노드를 부모와 직접 연결시킵니다.
- 즉, 부모가 자식을 "끌어올리는" 방식입니다
가장 복잡한 경우가 자식 노드가 2개인 경우입니다.

Case 3. 자식이 두 개인 경우
- 가장 복잡한 경우이며, 트리 구조를 유지하기 위해 특별한 처리가 필요합니다.
- 이 경우, Successor(후속 노드) 또는 Predecessor(선행 노드) 중 하나의 키 값을 가져와서 삭제할 노드에 복사한 뒤, Successor/Predecessor 노드를 대신 삭제합니다.
일반적으로 오른쪽 서브트리의 최소값인 Successor를 사용합니다.
이렇게 하면 이진 검색 트리의 조건(왼쪽 < 현재 노드 < 오른쪽)을 그대로 유지할 수 있습니다.
13을 삭제하려는 경우는 복잡해집니다. 하나인 경우에는 삭제하더라도 트리의 구조를 유지하고 복원할 수 있는데 둘인 경우에는 트리의 기본적인 구조 자체가 흐트러지기 때문에 조금 더 복잡할 수밖에 없습니다.
노드 13은 그대로 두고 데이터만 삭제할 것입니다. 그리고 다른 노드에 있는 데이터를 옮겨오는 것입니다. 이것이 바로 트리구조의 단점입니다. 만약 덩치가 크다면 다른 데이터를 가져와야 하므로 단점이 될 수 있는 것입니다. 하지만 트리를 만들 때 노드 안에 저장하는 경우보다 데이터 객체를 따로 만들고 노드에는 객체의 주소만 하는 경우도 반드시 그렇다는 건 아니지만 조금 더 일반적입니다.
노드는 그대로 두고 다른 노드에 저장된 데이터를 옮겨오겠다는 것입니다. 도대체 누구를 옮겨올 것인가? 라는 것이 문제가 됩니다. 그 경우에 누구를 이 자리로 가져오는 것이 간단할지 보면 binary search tree를 보면 크기들 간의 규칙이 있어야 합니다.
왼쪽 subtree는 작고 오른쪽은 나보다 크다라는 것을 유지해야 합니다.
presuccessor나 successor를 가져오면 됩니다. 여기에서 successor를 가져온다고 가정할 때, 삭제하고자 하는 노드가 자식이 둘인 경우므로 오른쪽 자식이 반드시 있으므로 오른쪽 sub에서 최소값을 찾으면 됩니다. 왼쪽으로 내려갈 수 없을 때까지 내려가면 됩니다.
먼저 13의 데이터만 삭제하고 successor를 찾아서 15를 옮겨오는 것입니다. 일단 원래 13이 있던 자리에 13의 successor가 왔다는 건 13보다 큰 값이 온 것이기에 왼쪽 트리 입장에선 불만이 없습니다. 13의 오른쪽 서브트리 입장에서도 전체에서 가장 작은 값이 올라갔으므로 남아있는 값들은 올라오는 것보다 클 것입니다.
successor를 찾아서 자리로 가져오게 되면 binary search트리가 유지해야 할 노드들의 저장된 데이터의 크기의 한계가 전혀 회손되지 않는다는 것을 알 수 있습니다.

case2처럼 노드를 삭제해주면 됩니다. 15를 찾아서 해주고 15는 트리로부터 삭제해주는 것입니다. successor를 찾아서 그 값을 삭제하려는 노드로 copy를 하고 Successor 노드를 대신 삭제해줍니다. 그러면 자식이 없거나 하나인 것이 됩니다.
TREE-DELETE(T, z)
if left[z] = NIL or right[z] = NIL
then y <- z
else y <- TREE-SUCCESSOR(z)
if left[y] != NIL
then x <- left[y]
else x <- right[y]
if x != NIL
then p[x] <- p[y]
if p[y] = NIL
then root[T] <- X
else if y = left[p[y]]
then left[p[y]] <- x
else right[p[y]] <- x
if y != z
then key[z] <- key[y]
copy y's satellite data into z
return y코드를 조심스럽게 따라가보면 실제로 삭제할 노드이며 y의 왼쪽 자식이 NULL이 아니라면 실제로 삭제할 노드이므로 적어도 y는 자식이 0개이거나 1개입니다. y가 원래 z라면 자식이 다르다면 success를 이유로 왼쪽 자식이 존재하지 않습니다. 왼쪽 자식이 존재하지 않는다면 즉 NULL이 아니라면 오른쪽 자식은 없다는 얘기이므로 왼쪽 자식이 존재한다면 즉 노드y의 자식은 0개이거나 1개입니다.
따라서 왼쪽 자식이 존재한다면 오른쪽 자식이 없는거고 아예 자식이 없을 수 있으니 그걸 고려하고 읽으면 됩니다.
이진검색트리는 높이는 o(log n) 입니다. 최악의 경우는 o(n)입니다.
이걸 개선한 것이 레드-블랙 트리이며 한쪽에 치우치지 않도록 해주며 O(log n)이 되도록 유지해줍니다. 하지만 삽입과 삭제가 복잡해집니다. 그 대가로 트리의 높이가 어떠한 경우에도 O(n)이 되도록 하지 않는 이진검색의 한 형태입니다.
'IT 프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘]이진트리의 순회 (0) | 2025.04.11 |
|---|---|
| [알고리즘] 최대 우선순위 큐, LowerBound (0) | 2025.04.09 |
| 트리 (0) | 2025.04.07 |
| [알고리즘] Heapsort (0) | 2025.03.28 |
| [알고리즘] mergesort (0) | 2025.03.27 |