그래프의 개념과 표현
그래프 G = (V,E)
- V : 노드(node) 혹은 정점(vertex)
- E : 노드쌍을 연결하는 엣지(Edge) 혹은 링크(link)
- 개체(object)들 간의 이진관계를 표현
- n = |V|, m = |E|

V={1,2,3,4,5,6,7,8}
E={(1,2),(1,3),(2,3),...,(7,8)}
n=8
m=11
방향 그래프와 가중치 그래프
방향 그래프(Directed Graph) G=(V,E)
- 에지(u,v)는 u로부터 v로의 방향을 가짐
가중치 그래프
- 에지마다 가중치(weight)가 지정
인접행렬
adjacency matrix


정점이 n개인 것을 n x n으로 표현한 것입니다. 1번부터 n번까지 모든 정점을 넘버링 한 것으로 I번째 행 J번째 열을 a_ ij라고 한다면 있으면 1 없으면 0으로 표시합니다.
1과 2사이에 edge가 있으므로 1행 2열의 값은 1입니다. 2행 1열의 값도 있으므로 1이 됩니다. 하지만 3과 4사이에 edge 가 없으므로 3행 4열은 0이 나옵니다.
edge가 있느냐 없느냐를 이런 식으로 표현할 수 있습니다.
어떤 노드 v에 인접한 모든 노드 찾기 : O(n) 시간
어떤 에지(u,v)가 존재하는지 검사 : O(1) 시간
인접리스트
- 정점 집합을 표현하는 하나의 배열과
- 각 정점마다 인접한 정점들의 연결 리스트
저장공간 : o(n+m)
어떤 노드 v에 인접한 모든 노드 찾기 : o(degree(v)) 시간
어떤 에지 (u,v)가 존재하는지 검사 : o(degree(u)) 시간
방향그래프
- 인접행렬은 비대칭
- 인접 리스트는 m개의 노드를 가짐
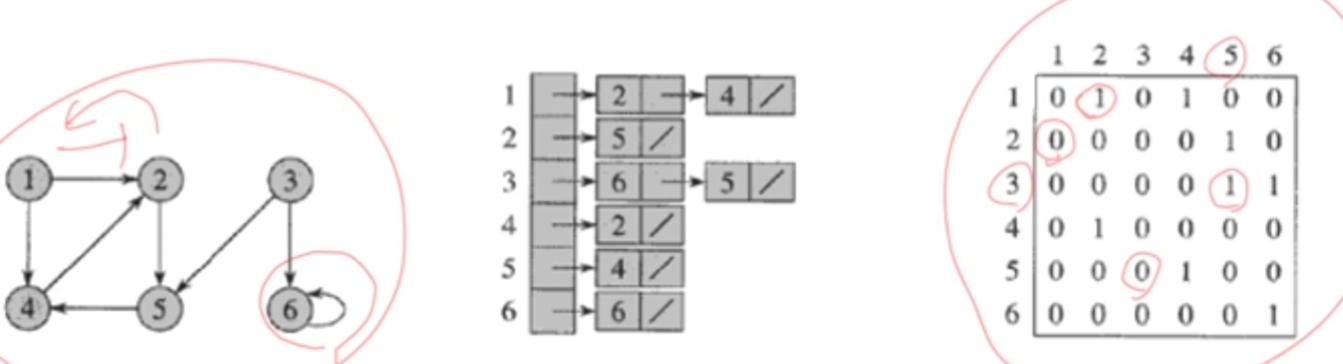
가중치 그래프의 인접행렬 표현
- 에지의 존재를 나타내는 값으로 1대신 에지의 가중치를 저장
- 에지가 없을 때 혹은 대각선:
- 특별히 정해진 규칙은 없으며, 그래프와 가중치가 의미하는 바에 따라서
- 예 : 가중치가 거리 혹은 비용을 의미하는 경우라면 에지가 없으면 무한대, 대각선은 0
- 예 : 만약 가중치가 용량을 의미한다면 에지가 없을 때 0, 대각선은 무한대
경로와 연결성
- 무방향 그래프 G=(V,E) 에서 노드 u와 노드 v를 연결하는 경로(path)가 존재할 때 v와 u는 서로 연결되어 있다고 말합니다.
- 모든 노드 쌍들이 서로 연결된 그래프를 연결된(connected) 그래프라고 합니다.
- 연결요소(connected component)

'IT 프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] DAG (0) | 2025.05.12 |
|---|---|
| [알고리즘] DAG (0) | 2025.05.10 |
| [알고리즘] 시간복잡도 (ppt) (0) | 2025.04.23 |
| [알고리즘]이진트리의 순회 (0) | 2025.04.11 |
| [알고리즘] 최대 우선순위 큐, LowerBound (0) | 2025.04.09 |