Directed Acyclic Graph
- DAG는 방향 사이클(directed cycle)이 없는 방향 그래프
- 예 : 작업들의 우선순위
위상정렬
DAG에서 노드들의 순서화 v1, v2, ... ,vn, 단, 모든 에지 (vi, vj)에 대해서 i<j가 되도록
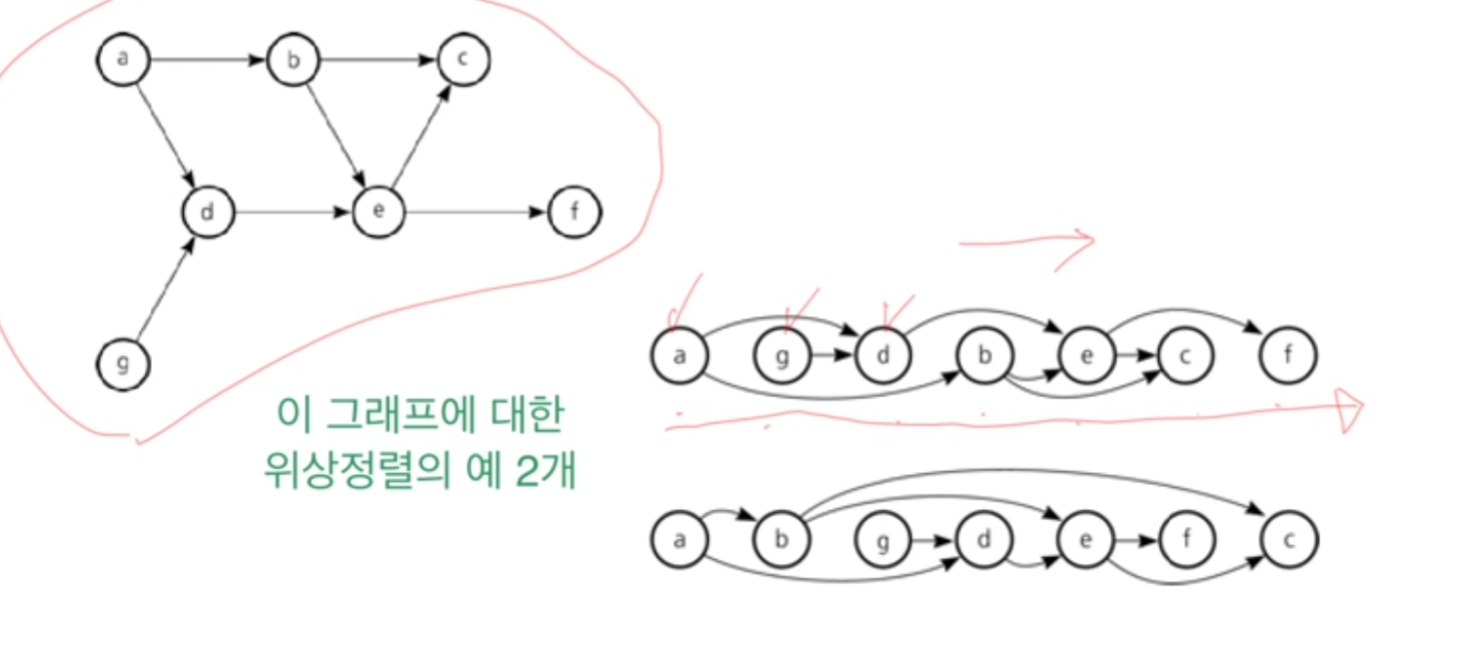
위상정렬은 답이 유효하진 않습니다.
indegree가 0인 것을 찾습니다. 이는 그 작업에 선행해야 하는 작업이 존재하지 않는 것입니다. a와 g는 아무때나 해도 상관없는 것입니다. 맨 처음에 a를 먼저 해도 된다는 것입니다. 그래프에서 indegree에서 0으로 하는 것이 제일 중요하구나 라는 것을 알아야 하며 두 개 이상 존재하면 그 중 하나를 출력합니다.
A에서 나가는 엣지들은 이제 생각할 필요 없습니다. 남은 그래프에서 indegree가 0인 것을 찾으면 g와 b가 있으면 그 중 아무거나 먼저 한 다음 g에서 나가는 edge도 의미가 없으므로 A를 출력하고 A에서 나가는 edge들을 제거하고 G를 출력하고 G에서 나가는 edge들을 제거하면 됩니다.
topologicalSort1(G)
{
for <- 1 to n {
진입간선이 없는 임의의 정점 u를 선택한다;
A[i] <-= u;
정점 u와 u의 진출간선을 모두 제거한다;
}
배열 A[1..n]에는 정점들을 위상정렬 되어 있다.
}
수행시간 : O(n+m)진입간선 Indegree가 0인 u를 선택해야 합니다.
1) indegree = 0인 노드가 존재하지 않으면? (수업시간에 질문)
위상정렬 알고리즘 2
topologicalSort2(G)
{
for each v⊂V
VISITED[V] <- NO;
make an empty linked list R;
for each v⊂V 정점의 순서는 상관없음
if (visited[v] = NO) then
DFS-TS(v, R);
}
DFS-TS(v, R)
{
visited[v] <- YES;
for each x adjacent to v do
if (visited[x] = NO) then
DFS-TS(x, R);
add v at the front of the linked list R;
}알고리즘이 끝나면 연결 리스트 R에는 정점들이 위상정렬된 순서로 매달려 있다. O(n+m)
아무노드나 하나 선택합니다. DFS를 할 때 이 노드에서 나가는 것은 하나밖에 없기 때문에 1이 됩니다. 방향그래프이기에 할 수 있는 것이 없으니 빠져나갑니다.

자기자신을 연결리스트의 맨 앞에 넣는 것입니다. R-> 계란
이 노드에서 할 일이 없으니 recursion에서 종료되면 전 노드인 수프넣기로 돌아옵니다. 이 노드에서도 역시 더이상 갈 곳이 없기에 자기자신이 연결리스트 R의 맨앞에 추가합니다. 노드가 하나 붙어있으므로 그 앞에 수프넣기를 추가하면 됩니다. 그리고 갈 수 있는 곳이 없으므로 종료되고 FOR문으로 돌아옵니다. for each v로 돌아와서 VISITED가 0인 것을 찾아서 dfs를 시작합니다.
2개를 제외한 나머지 노드 중에서 아무거나 하나를 택해서 와서 보니깐 갈 수 있는 노드는 하나박에 없는데 체크되어 있기 때문에 막다른 골목이 됩니다. 그러면 자기자신을 연결리스트 R을 맨앞에다 추가하고 역시 Recursion이 return 되어서 돌아옵니다. 여기에서 인접한 노드는 셋 다 체크되어 있기에 더이상 갈 곳이 없어서 자기자신을 연결리스트에 추가합니다.
그래서 종료하고 다시 DFS가 종료되고 for문으로 돌아옵니다. 여전히 visited가 0인 것을 검사해보고 라면 봉지 뜯기가 unvisited가 될 것이기 때문에 이것을 호출하면 호출되는 즉시 종료되며 자기자신이 맨 앞의 연결리스트에 됩니다.
Graph에서 unvisited 노드가 남아있지 않을 때까지 모든 정점들을 하나의 연결리스트로 만들기 때문에 정점들이 하나의 연결리스트로 만들어집니다. 이 연결리스트가 위상정렬이다 라는 것인데 위상정렬이 아니라고 가정을 해보면 이 리스트 상에 역방향의 edge가 존재한다는 것입니다.
위상정렬이 아니라면 리스트 상에 뒤쪽 정점으로부터 앞쪽 정점으로 가는 edge가 존재한다는 것인데 조금 생각해보면 그것이 존재할 수 없다는 것을 알 수 있습니다.
이것을 언제 삽입했는지 보면 DFS를 해서 더이상 갈 곳이 없을 때 추가로 방문한 노드가 없을 때 라면 넣기를 연결리스트에 넣기 때문에 앞쪽으로 가는 Edge가 있다면 앞쪽에 있는 예는 라면넣기보다 나중에 추가되었으니 이 라면넣기를 연결리스트에 추가하는 그 시점에 아직 visited 되지 않은 노드였다는 것이고 그런 edge가 있다면 노드르 방문을 했을 것이기 때문에 앞쪽에 삽입될 수는 없습니다.
이런 사실을 생각해보면 이렇게 만들어지는 연결리스트가 위상정렬이 될 수 밖에 없다는 것을 알 수 있습니다. 완전하게 알고리즘에 대해 직관적인 이해에 도달하기 위해선 조금 생각해볼 필요가 있습니다.
DFS를 시작해서 DFS의 막다른 골목까지 간 것이 계란이며 더이상 갈 곳이 없으면 도달하면 Return되어서 도달아옵니다. 이런 DFS의 본성과 알고리즘을 이해하는 것이 필요합니다.
가장 논리적인 증명은 결과적으로 찾아진 연결리스트에서 역방향의 edge가 존재할 수 없다는 것입니다.
---
수정하기
--- 권오흠교수님 강의 발췌록
'IT 프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 최소 비용 신장 트리 ( MST ) (0) | 2025.05.14 |
|---|---|
| [알고리즘] DAG (0) | 2025.05.12 |
| 그래프 (0) | 2025.05.08 |
| [알고리즘] 시간복잡도 (ppt) (0) | 2025.04.23 |
| [알고리즘]이진트리의 순회 (0) | 2025.04.11 |