- 입력 : n개의 도시, 도시와 도시를 연결하는 비용
- 문제 : 최소의 비용으로 모든 도시들이 서로 연결되게 한다.

해가 유일하지는 않음
예 : (b, c) 대신 (a, h)

왜 트리라고 부르는가?
- 싸이클이 없는 연결된 무방향 그래프를 트리라고 부른다.
- MST 문제의 답은 항상 트리가 됨 왜?
Generic MST 알고리즘
- 어떤 MST의 부분집합 A에 대해서 Au{(u,v)}도 역시 어떤 mst의 부분 집합이 될 경우 에지(u,v)는 A에 대해서 안전하다고 합니다.
- Generic MST 알고리즘
1. 처음에는 a =공집합으로 합니다.
2. 집합 a에 대해서 안전한 에지를 하나 찾은 후 이것을 a에 더한다.
에지의 개수가 n-1이 될 때까지 2번을 반복한다.
안전한 에지 찾기
- 그래프의 정점들을 두 개의 집합 s와 v-s로 분할한 것을 컷이라고 부른다.
- 에지 (u,v)에 대해서 u 부분집합 s이고 v 부분집합 v-s 일 때 에지 (u,v)는 컷 (s, v-s)를 cross한다고 말합니다.
- 에지들의 부분집합 A에 속한 어떤 에지고 컷 (s, v-s)를 cross하지 않을 때 컷 (s, v-s)는 a를 존중한다고 말합니다.

노드들을 두 그룹으로 분할한 것을 cut이라고 부름
한 그룹에서 다른 그룹으로 건너가는 과정을 cut을 cross하는 에지라고 부릅니다.
edge들의 A를 존중하는 것이라는 것은 어떤 빨간 에지도 CROSS하지 않을 때 집합 A를 존중한다고 말합니다.
Kruskal의 알고리즘
- 에지들을 가중치의 오름차순으로 정렬한다.
- 에지들을 그 순서대로 하나씩 선택해간다. 단, 이미 선택된 에지들과 사이클을 형성하면 선택하지 않는다.
- n-1개의 에지가 선택되면 종료한다.


사이클이 만약 선택되면 포기합니다.
왜 이렇게 하면 MST가 찾아지는가?
- Kruskal의 알조리즘의 임의의 한 단계를 생각해보자
- A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자

사이클을 만들지 않으면서 Weight가 최소인 것을 선택해야 합니다. 에지의 부분집합 A가 MST의 부분집합이고, A를 존중하는 임의의 컷이 있을 때 어떤 edge도 cross하지 않을 때, 이 edge를 추가하더라도 MST의 일부라는 것을 가져와서
빨간 Edge들이 Kruskal의 알고리즘이 선택한 edge라고 할 때, u, v가 사이클을 만들지 않는 작은 edge일 때, u,v는 빨간 edge들에 의해서 만들어지는 u와 v는 적어도 빨간 edge들에 의해서 연결되지 않았다 라는 것은 당연한 얘기입니다.
u와 v가 빨간 엣지들에 의해서 연결되어 있었다면 선택하는 순간 싸이클이 만들어집니다.
u,v를 선택하더라도 사이클이 만들어지지 않는다는 것이니 u와 v가 아직 연결되어있지 않다는 것입니다. 그렇기 때문에 빨간 edge들에 의해서 연결되지 않은 것을 s라고 하고 나머지 모든 정점들을 V-S라고 하게 되면 이 두 컷을 Cross하는 어떤 edge도 사이클을 만들지 않을 것입니다.
한 쪽은 s에 속해있고 한 쪽은 v-s에 속해 있기에 아직 서로 연결되지 않은 노드라는 뜻이고 따라서 그런 edge를 추가하더라도 사이클을 만들지 않습니다. 즉 kruskal의 알고리즘이 고를 수 있는 후보가 되는 edge입니다.
이 edge가 그런 edge에서 weight가 최소인 edge이니 edge들의 부분집합 a의 cut에 대해 cross하지 않은 weight가 작은 edge가 kruskal알고리즘입니다. Kruskal 엣지 e는 안전하고 A에다가 e를 추가하더라도 MST의 u,v 존재한다는 것입니다.
Kruskal 알고리즘 구현 핵심
사이클 검사
- 초기 상태 : 선택된 에지 없음
- 각각의 연결요소를 하나의 집합으로 표현

그래프에서 weight가 최소인 것을 찾아서 다른 집합에 속하므로 edge를 선택하고 g가 속한 집합과 h가 속한 집합을 합집합하여 하나의 집합으로 만들어줍니다.
이렇게 계속 다른 집합에 속하고 사이클이 되지 않는 것에 대해서 연결해줍니다. 이렇게 하면 MST가 찾아집니다.
서로소인 집합들의 표현
- 각 집합을 하나의 트리로 표현
- 예 : 2개의 집합

각각의 집합을 하나의 트리로 표현을 합니다. 두개의 집합이 있으면 각각을 하나의 트리로 표현하는데 트리에서 모든 노드는 부모가 유일합니다. 따라서 각각의 노드는 유일한 자기 노드의 주소를 가지기 때문에 생각처럼 복잡한 자료구조는 아닙니다.
disjoint한 집합을 표현하기 위해 상향식 트리로 표현합니다.

모든 트리를 하나의 배열로 표현할 수 있습니다.

disjoint set을 트리로 했다면 find-set이라는 것은 어떤 노드 v에 대해서 v가 속해있는 집합을 알아내는 것입니다. 집합에다가 따로 이름을 부여하지는 않을 것입니다.
루트 노드의 이름을 그 집합의 이름으로 두 노드가 동일한 집합에 속해있느냐 아니느냐가 필요한 것이기에 이름을 부여할 필요는 없고 그 원소가 속해있는 트리의 루트, 다른 원소에 대해서 그 노드가 속해있는 트리의 루트를 봐서 두 루트노드가 동일하면 같은 집합이고 다르면 다른 집합입니다.
FIND-SET (x)
if x != p[x]
then p[x] <- FIND-SET(p[x])
return p[x]루트까지 오게 되면 자신과 자신의 부모가 동일한 것입니다. 그래서 recursion으로 구현한 것입니다. O(h), h는 트리의 높이 h는 최악의 경우 O(n)
x가 루트가 아니라면 x가 속해있는 루트는 x의 부모가 속해있는 루트와 동일할 것입니다. x가 자기 부모와 다르다면 자기 부모가 속해있는 부모의 recursion을 찾으면 됩니다. 이것을 recursion으로 구현하지 않고 반복문으로 구현한다면 while(x != p(x)) x = p(x); return x; 혹은 p(x) 이렇게 반복문으로 구현할 수도 있을 것입니다.
이것이 find-set연산입니다.
union(u,v)
- 한 트리의 루트를 다른 트리의 루트의 자식 노드로 만듬
UNION(u,v)
x <- FIND-SET(u);
y <- FIND-SET(v);
p[x] <- y;루트 노드를 찾은 이후에는 O(1), 하지만 루트를 찾는데 O(h)
Weighted union
find 알고리즘의 시간복잡도가 트리의 높이에 비례한다는 것입니다. 가능한 한 트리의 높이가 낮아지도록 만드는 것이 목적입니다. union을 할 때 Weighted union이라는 간단한 알고리즘 만으로도 큰 향상을 이룰 수 있는데
- 두 집합을 union할 때 작은 트리의 루트를 큰 트리의 루트의 자식으로 만듬 (여기서 크기란 노드의 개수)
- 각 트리의 크기(노드의 개수)를 카운트하고 있어야 함
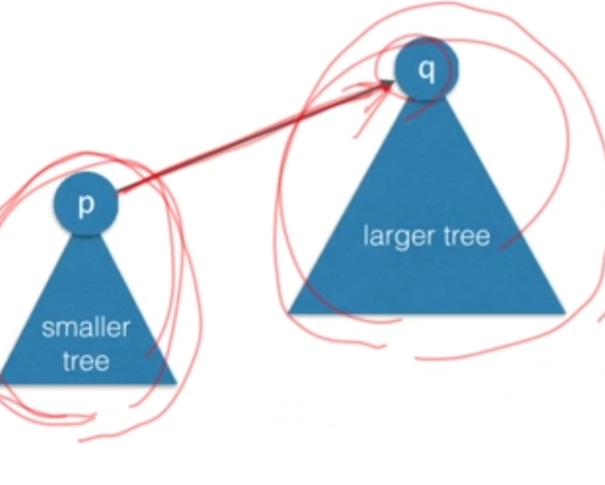
WEIGHTED-UNION(u,v)
x <- FIND-SET(u);
y <- FIND-SET(v);
if size[x]>size[y] then
p[y] <- x;
size[x] <- size[x] + size[y];
else
p[x] <- y;
size[y] <- size[y] + size[x];
Worst vs Weighted Union
union을 할 때 최악을 할 때 아닌 경우와 트리의 모양이 어떻게 변해가는지 그림으로 그린 것입니다.
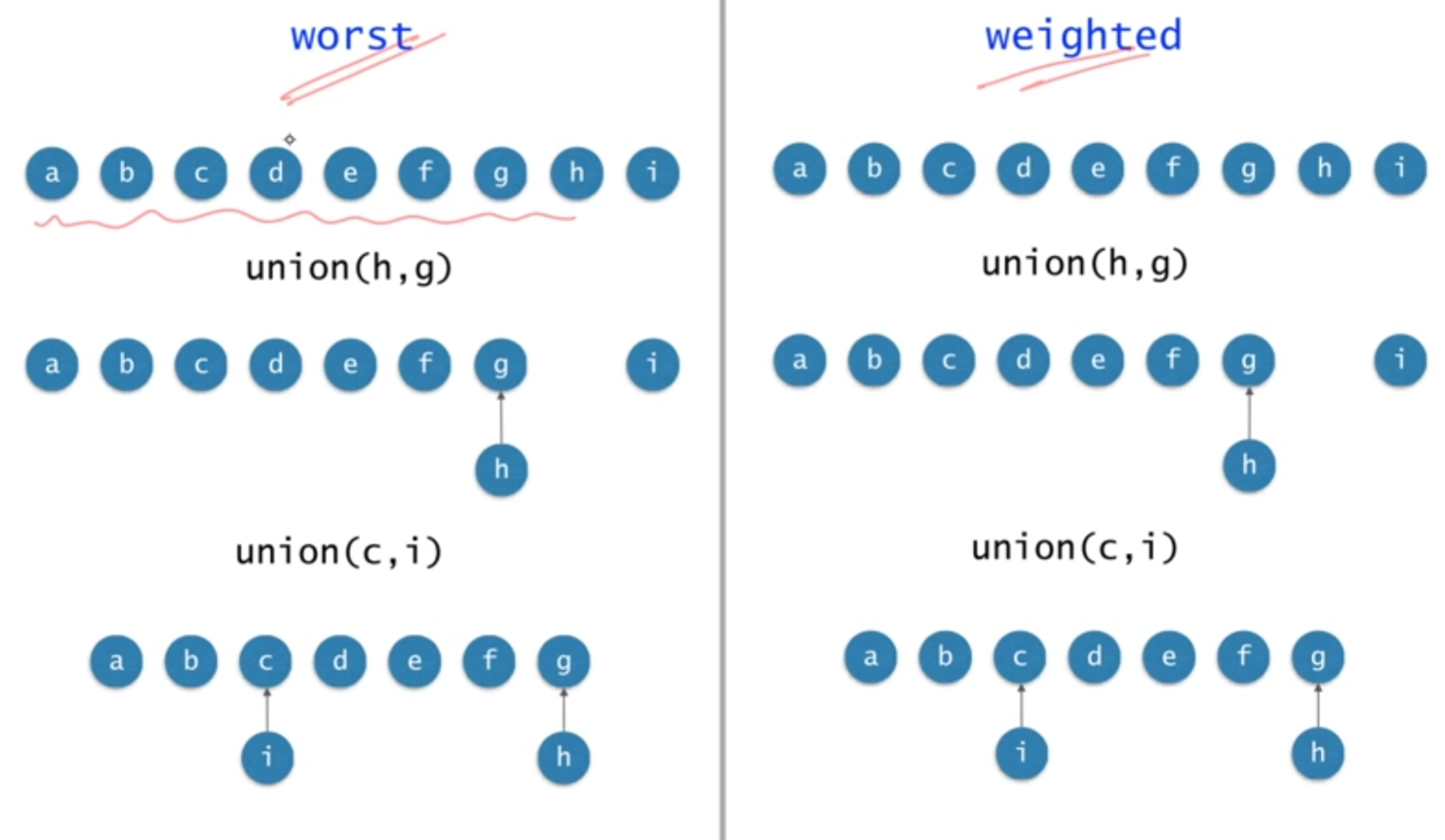

weighted union을 하게 되면 log(n)을 넘지 않게 됩니다. 왜 그러냐하면 어떤 노드가 맨 처음에는 다 독립된 트리로 시작을 하기 때문에 어떤 트리의 높이가 1이지만 트리의 높이가 2가 되기 위해서는 내가 속한 트리와 다른 트리가 합쳐져서 1이 증가한다면 합쳐진 두 트리 중 작은 쪽에 속해있어야 합니다.
두개의 트리를 합쳐서 할 때 다른 노드들의 레벨은 전혀 변화가 없고 union을 할 때 레벨이 증가하는 노드는 e가 유일합니다. 레벨 0인데 레벨 1이 되었습니다.
union을 할 때 작은 쪽에 속해 있을 때만 레벨이 1 증가합니다. 두 개의 트리를 합칠 때, 모든 노드들이 자기 혼자인 트리에서 출발해서 merge 해서 어떤 노드의 레벨이 h가 되었다 그러면 레벨이 1이던 애가 2가 됐다는 것은 자기가 속해있던 트리가 다른 트리와 합쳐졌다는 것입니다.
자기와 합쳐진 트리가 내가 합쳐진 트리와 노드가 많을 때만 레벨이 증가합니다. 노드의 개수가 n개일때 h는 log n입니다.
Path Compression
Find를 할 때 하는 일입니다.
FIND-SET-PC(x)
while x != p[x] do
p[x] <- p[p[x]];
x <- p[x];
end.
return p[x];g를 루트의 자식으로 f를 루트의 자식으로 path compression 압축을 하는 것입니다.
Weighted union with path compression (wupc)
- m번의 union-find 연산의 총 시간복잡도는 o(N+M log *N) 여기서 N은 원소의 개수
- 거의 선형시간 알고리즘, 즉 한 번의 Find 혹은 Union이 거의 O(1) 시간
log *N = log를 몇번 취하면 1이 되느냐 입니다. log * 2 는 1이 됩니다. 4에다가 log를 한번 취하면 2로 2번 취하면 1이 되므로 log * 4 는 2가 됩니다. log * 16 = 3이 됩니다. log * n이 4가 되려면 log 무언가를 해서 16이 되어야 하는 값이므로 2^16 입니다. 이는 대략 65636입니다. log * n = 5가 되려면 이는 2^65536이 됩니다.
Prim의 알고리즘
- 임의의 노드를 출발 노드로 선택
- 출발 노드를 포함하는 트리를 점점 키워 감
- 매 단계에서 이미 트리에 포함된 노드와 포함되지 않은 노드를 연결하는 에지들 중 가장 가중치가 작은 에지를 선택

왜 MST가 찾아지는가?
- Prim의 알고리즘의 임의의 한 단계를 생각해본다
- A를 현재 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정

어떻게 구현할지 생각해보면 prim의 알고리즘에서 중요한 것은 까만 노드들과 하얀 노드들을 연결하는 엣지들 중에서 weight가 최소인 부분을 찾는 것입니다.
일반적으로 전체 노드의 개수가 n개인데 n/2 개 정도가 v에 속해있고 나머지 절반이 속하지 않았다면 이 둘을 연결하는 노드는 최악의 경우에는 (n/2)^2 즉 모든 쌍끼리 edge가 있는 경우가 있습니다.
o(n^2)개의 엣지를 찾아야 한다는 것입니다. 이 중에서 엣지가 8개 중에서 최소인 것을 찾아야 하기에 한 스텝에서 필요한 시간복잡도가 최악의 경우 o(n^2)이 되는데 이걸 n-1개 찾아야 하므로 별 생각없이 단순하게 구현한다면 시간복잡도는 o(n^3) 이겠지만 이는 바람직하지 않습니다.
어떻게 하면 줄일 수 있을지 생각해보면 가중치가 최소인 엣지를 찾아야 합니다.
- Va : 이미 트리에 포함된 노드들
- Va에 아직 속하지 않은 각 노드 v에 대해서 다음과 같은 값을 유지
- key(v) : 이미 Va에 속한 노드와 자신을 연결하는 에지들 중 가중치가 최소인 에지(u,v)의 가중치
- 파이(V) : 그 에지 (u,v)의 끝점 u
가중치가 최소인 에지를 찾는 대신 key값이 최소인 노드를 찾는다.
하지만 모든 key값을 계산했다는 가정하에서는 o(n)의 시간이 걸리겠지만 key값을 계산하는데 시간이 걸립니다. key 값을 계산하는 방법은 맨 처음에는 그래프에서 출발점만이 Va에 속하고 나머지 모든 노드들이 Va에 속하지 않습니다.
맨 처음에 각 노드의 key값은 Va에 속한 노드와 엣지중에 가벼운 엣지인데 Va에 속한 노드가 출발점으로 유일하므로 각각의 노드의 key값은 출발점과 edge가 있으면 그것의 weight가 될 것이고 없다면 key값은 무한대가 될 것입니다.
애초에 초기화 과정에서 모든 노드의 key값을 계산하는 것을 O(n)시간이면 충분합니다. 연결되어 있으면 에지의 weight 아니면 무한대 초기화 하면 되는 것입니다.
edge를 하나 찾을 때마다 갱신해주면 되는데 매번 노드의 key값을 새로 계산하는 것이 아니라 각 노드의 key값을 조금 전에 있던 key값으로부터 필요한 노드들에 대해서만 갱신해주면 됩니다.
그렇게 갱신하는데 걸리는 시간은 O(n)이면 충분합니다.

prim의 알고리즘을 효과적으로 구현하기 위한 다른 방식 중 하나는 최소 우선순위 큐입니다. Minimum priority Queue
- V-Va에 속한 노드들을 저장
- Extract-Min : key값이 최소인 노드를 삭제하고 반환
extreact max , insert - o(log n)

이진 힙을 사용하여 우선순위 큐를 구현한 경우
while loop
- n번의 Extract-min : o(nlogn)
- m번의 decrease-key : o(mlogn)
따라서 시간복잡도 : o(nlogn+mlogn) = o(mlogn)
우선순위 큐를 사용하지 않고 단순하게 구현할 경우 o(n^2)
Fibonacci 힙을 사용하여 o(m+nlogn)에 구현 가능
'IT 프로그래밍 > 알고리즘' 카테고리의 다른 글
| [알고리즘] DAG (0) | 2025.05.12 |
|---|---|
| [알고리즘] DAG (0) | 2025.05.10 |
| 그래프 (0) | 2025.05.08 |
| [알고리즘] 시간복잡도 (ppt) (0) | 2025.04.23 |
| [알고리즘]이진트리의 순회 (0) | 2025.04.11 |