객체지향 프로그래밍 25번 , 26번, 28번, 29번, 30번, 31번, 32번, 33번

IT 프로그래밍/객체지향프로그래밍

객체지향 프로그래밍 25번 , 26번, 28번, 29번, 30번, 31번, 32번, 33번

기술1 2024. 4. 20. 16:32

#include <iostream>

using namespace std;

const int MAX = 100;

int main() {
    int n;
    cin >> n;
    int data[MAX];

    // 입력 받은 정수를 배열에 저장
    for (int i = 0; i < n; i++) {
        cin >> data[i];
    }

    // 버블 정렬을 사용하여 배열을 오름차순으로 정렬
    for (int i = n - 1; i > 0; i--) {
        for (int j = 0; j < i; j++) {
            if (data[j] > data[j + 1]) {
                int tmp = data[j];
                data[j] = data[j + 1];
                data[j + 1] = tmp;
            }
        }
    }

    // 중복된 값을 제거하고 남은 값을 새로운 배열에 저장
    int uniqueData[MAX];
    int uniqueCount = 0;
    for (int i = 0; i < n; i++) {
        if (i == 0 || data[i] != data[i - 1]) {
            uniqueData[uniqueCount++] = data[i];
        }
    }

    // 중복 제거된 값들의 개수와 값을 출력
    cout << uniqueCount << ": ";
    for (int i = 0; i < uniqueCount; i++) {
        cout << uniqueData[i] << " ";
    }
    
    return 0;
}

일단 버블정렬로 함수를 정렬시켜 줍니다.

이후 for문을 통해 uniquedata 라는 배열을 만들어 준 다음 거기에 중복된 수가 아닌 다른 수만 나오게끔 정렬을 해주면 됩니다.

#include <iostream>

using namespace std;

const int MAX = 100;
int main()
{
	int s[MAX], t[MAX], n;
	cin >> n;

	for (int i = 0; i < n; i++)
		cin >> s[i] >> t[i];

	for (int i = n - 1; i > 0; i--)
	{
		for (int j = 0; j < i; j++)
		{
			if (s[j] > s[j + 1] || s[j] == s[j + 1] && t[j] > t[j + 1])
			{
				int tmp = s[j];
				s[j] = s[j + 1];
				s[j + 1] = tmp;
				tmp = t[j];
				t[j] = t[j + 1];
				t[j + 1] = tmp;
			}
		}
	}

	for (int i = 0; i < n; i++)
		cout << s[i] << " " << t[i] << endl;
	return 0;
}

입력으로 받은 시간 범위들을 배열 s와 t에 저장합니다. s배열은 시작 시간을 ,t 배열은 종료 시간을 저장합니다. 그런 다음 버블정렬을 사용하여 시간 범위들을 정렬합니다. 정렬 과정에서 시작 시간이 우선적으로 비교되며, 시작 시간이 같은 경우 종료 시간을 비교하여 정렬합니다.

정렬된 결과를 출력합니다.

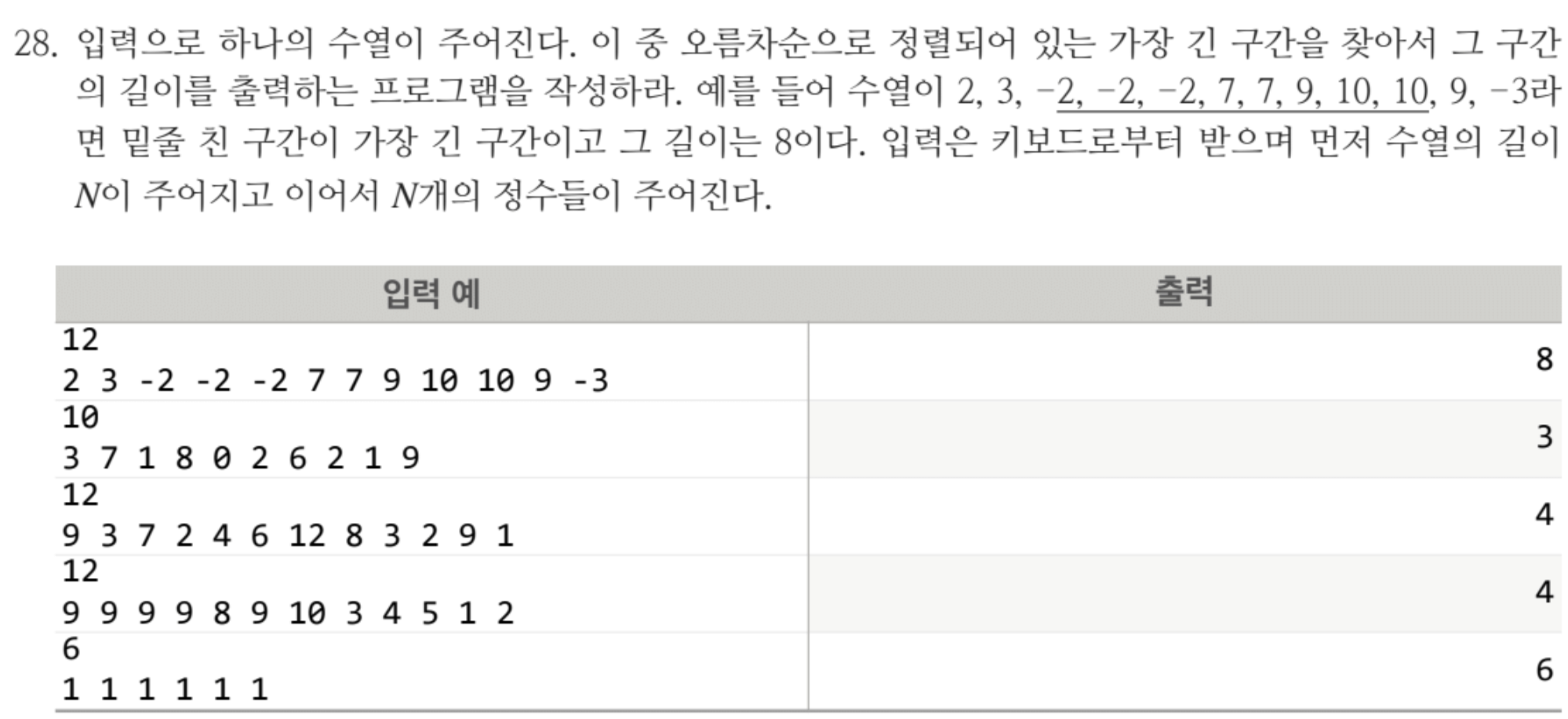
#include <iostream>

using namespace std;

const int MAX = 100;
int main()
{
	int n, num[MAX];

	cin >> n;
	for (int i = 0; i < n; i++)
		cin >> num[i];

	int max_len = 1, len = 1;
	for (int i = 1; i < n; i++)
	{
		if (num[i] >= num[i - 1])
			len++;
		else
			len = 1;
		if (len > max_len)
			max_len = len;
	}
	cout << max_len;

	return 0;
}

이 코드는 그저 따라해보면 나올 것이다. 어렵지 않은 코드기에 설명은 생략해도 될 것 같다.

#include <iostream>

using namespace std;

const int MAX = 100;

int main() {
    int n, k, num[MAX];

    // 배열의 크기와 요소들을 입력 받음
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> num[i];

    // 합이 될 값 k를 입력 받음
    cin >> k;

    int sum = 0, max_len = 0;
    int s = 0;
    for (int i = 0; i < n; i++) {
        sum += num[i];
        while (sum > k) {
            sum -= num[s++];
             
            if (i - s + 1 > max_len)
                max_len = i - s + 1;
        }
    }

    // 최대 길이 출력
    cout << max_len;

    return 0;
}

여기서 주목할 부분은 마지막에 배열의 각 요소를 순회하면서 배열의 합을 나타내는 값을 구하는 알고리즘일 것입니다. sum에 현재 요소 num[i]를 더하는 것으로 시작됩니다. 그리고 while루프를 사용하여 sum이 k를 초과하는지 확인합니다.

만약 sum이 k를 초과한다면 즉 sum에서 가장 첫 번째 요소를 빼고 ' sum -= num[s++]; 첫 번째 요소의 인덱스 s를 증가시켜서 부분배열의 길이를 줄입니다.

그리고 if문을 사용하여 현재 부분 배열의 길이가 이전에 저장된 최대 길이보다 길 경우, 최대 길이를 업데이트합니다.

이 코드의 핵심은 슬라이딩 윈도우 기법을 사용하여 배열을 순회하면서 합이 'k'를 초과하지 않는 부분배열을 찾는 것입니다. 이는 부분 배열의 시작 인덱스를 가리키는 s를 조절하여 부분열의 길이를 조절함으로써 이루어집니다.

예를 들어, 배열 [1, 2, 3, 4, 5]에서 k가 10일 때를 생각해봅시다.

초기에는 부분 배열이 [1]에서 시작합니다. 합은 1이므로 k를 초과하지 않습니다.

다음으로 부분 배열은 [1, 2]가 됩니다. 합은 3이므로 k를 초과하지 않습니다.

이어서 부분 배열은 [1, 2, 3]이 됩니다. 합은 6이므로 k를 초과하지 않습니다.

그러나 [1, 2, 3, 4]로 확장될 때 합이 10을 초과하게 됩니다.

따라서 가장 첫 번째 요소를 빼고, 부분 배열은 [2, 3, 4]가 됩니다. 이 과정을 계속 반복하면서 최대 길이를 찾게 됩니다.

#include <iostream>

using namespace std;

const int MAX = 100;

int calc_overlap(int s1, int t1, int s2, int t2)
{
    if (t1 <= s2 || t2 <= s1)
        return 0;
    return min(t1, t2) - max(s1, s2);
}

int main() {
    int s[MAX], t[MAX], n;
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> s[i] >> t[i];

    int max_len_overlap = 0;
    int max_i = 0, max_j = 0;

    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            int len = calc_overlap(s[i], t[i], s[j], t[j]);
            if (len > max_len_overlap)
            {
                max_len_overlap = len;
                max_i = i, max_j = j;
            }
        }
    }
    cout << s[max_i] << " " << t[max_i] << " " << s[max_j] << " " << t[max_j];

    return 0;
}

위 코드는 주어진 시간 범위들 중에서 겹치는 부분이 가장 긴 두 개의 시간 범위를 찾아 출력하는 프로그램입니다. 여기서 calc_overlap 함수는 두 개의 범위가 겹치는 길이를 계산합니다. 두 개의 범위가 겹치지 않으면 0을 반환하고, 겹친다면 겹치는 부분의 길이를 반환합니다.

main 함수에서는 모든 범위 쌍을 비교하여 겹치는 부분이 가장 긴 두 개의 범위를 찾습니다. 이때 calc_overlap 함수를 사용하여 겹치는 길이를 계산하고, 가장 긴 겹치는 길이를 찾아 해당 시간 범위 인덱스를 저장합니다.

최종적으로 가장 긴 겹치는 부분을 가지고 있는 두 개의 시간 범위의 시작 시간과 종료 시간을 출력합니다.

위 코드는 주어진 범위들 중에서 겹치는 부분이 가장 긴 두 개의 시간 범위를 찾는 것을 수행하고 있습니다.

int calc_overlap(int s1, int t1, int s2, int t2)
{
    if (t1 <= s2 || t2 <= s1)
        return 0;
    return min(t1, t2) - max(s1, s2);
}

두 개의 범위가 주어졌을 때 두 범위를 겹치는 길이를 계산하는 것입니다.

1. 첫 번째 범위가 두 번째 범위보다 먼저 발생하거나 두 번째 범위가 첫 번째 범위보다 먼저 발생하면 두 범위는 겹치지 않습니다. 즉 t1이 s2보다 작거나 t2가 s1보다 작거나 같으면 두 범위는 겹치지 않습니다.

즉 t1이 s2보다 작거나 같거나, t2가 s1보다 작거나 같으면 두 범위는 겹치지 않아서 겹치는 길이는 0이됩니다.

2. 그렇지 않으면 두 범위가 겹치는 부분이 존재합니다. 이때 겹치는 부분의 길이를 계산하기 위해 다음과 같이 계산합니다.

1) 겹치는 부분 시작은 두 범위 중에서 더 늦은 것이기 때문에 max(s1, 2)가 겹치는 부분의 시작이 됩니다. 겹치는 부분의 종료는 두 범위 중에서 더 빠른 종료이므로 min(t1, t2)가 겹치는 부분의 종료가 됩니다.

이때 겹치는 부분의 길이를 계산하려면 종료에서 시작을 빼면 됩니다. 즉 min(t1, t2)에서 max(s1, s2)를 빼면 됩니다.

#include <iostream>

using namespace std;

const int MAX = 100;


int main() {
    int flags[14] = { 0, };
    int k;

    for (int i = 0; i < 7; i++)
    {
        cin >> k;
        flags[k] = 1;
    }
    int count = 0;

    for (int i = 1; i <= 13; i++)
    {
        if (flags[i] == 1)
            count++;
        else
            count = 0;

        if (count == 5)
        {
            cout << "YES";
            return 0;
        }
    }
    cout << "NO";
    return 0;
}

해당 코드는 보면 바로 이해가 될 만큼 간단명료 하기 때문에 크게 설명할 것은 없습니다.

#include <iostream>

using namespace std;

const int MAX = 100;


int main() {
    int seq[MAX], n;
    int forward[MAX] = { 0 }, backward[MAX] = { 0 };
    cin >> n;

    for (int i = 0; i < n; i++)
        cin >> seq[i];
    for (int i = 1; i < n; i++)
    {
        if (seq[i - 1] == 0)
            forward[i] = 0;
        else
            forward[i] = forward[i - 1] + 1;
    }

    for (int i = n - 2; i >= 0; i--)
    {
        if (seq[i + 1] == 0)
            backward[i] = 0;
        else
            backward[i] = backward[i + 1] + 1;
    }

    int max = 0;
    for (int i = 0; i < n; i++)
    {
        if (forward[i] + backward[i] + 1 > max)
            max = forward[i] + backward[i] + 1;
    }
    cout << max;
    return 0; 
}

seq 배열은 입력된 수열을 저장하고, n은 수열의 길이를 나타냅니다.
forward 배열은 각 위치에서 왼쪽으로 연속된 1의 개수를 저장합니다. 만약 현재 위치의 왼쪽에 0이 나오면 연속된 1의 개수를 초기화합니다.
backward 배열은 각 위치에서 오른쪽으로 연속된 1의 개수를 저장합니다. 만약 현재 위치의 오른쪽에 0이 나오면 연속된 1의 개수를 초기화합니다.
수열을 순회하면서 각 위치에서 왼쪽과 오른쪽으로 연속된 1의 개수를 합하여 가장 큰 값을 찾습니다. 이 때, 현재 위치에 있는 0을 1로 바꾸었을 때의 연속된 1의 개수를 구합니다.
마지막으로 최대값을 출력합니다.

여기서 중요한 점은 두 번의 반복문을 사용하여 왼쪽과 오른쪽 방향으로 연속된 1의 개수를 각각 구하고, 이를 합하여 현재 위치에서 0을 1로 바꿨을 때의 가장 긴 연속된 1의 길이를 찾는 것입니다.

예를 들어, 입력된 수열이 {1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1} 일 때, 가장 긴 연속된 1의 개수를 구하는 과정을 살펴보면 다음과 같습니다:

forward 배열: {0, 1, 0, 0, 0, 1, 0, 1, 2, 0, 1, 2, 3}
backward 배열: {3, 2, 1, 0, 3, 2, 1, 0, 0, 3, 2, 1, 0}
각 위치에서 forward와 backward 값을 합하여 최대값을 찾으면, 최대 연속된 1의 개수는 7이 됩니다.

따라서 위 코드는 입력된 수열에서 하나 이하의 0을 1로 교체하여 만들 수 있는 가장 긴 연속된 1의 개수를 구하는 프로그램입니다.

#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;
const int MAX = 100;

void reset();
bool is_blocked(int x, int y);
bool feasible_dir(int x, int y, int dir);

int maze[MAX][MAX], N;;
int offset[4][2] = { {-1, 0}, {0, 1}, {1, 0}, {0, -1} };
int main() {

    srand((unsigned int)time(NULL));
    cin >> N;
    int count = 0;
    for (int t = 0; t < 10000; t++) {
        int x = N / 2, y = N / 2;
        reset();
        maze[x][y] = 1;
        bool escaped = false;
        while (1) {
            if (x == 0 || y == 0 || x == N - 1 || y == N - 1) {
                escaped = true;
                break;
            }
            if (is_blocked(x, y))
                break;
            int dir = rand() % 4;
            if (feasible_dir(x, y, dir)) {
                x += offset[dir][0];
                y += offset[dir][1];
                maze[x][y] = 1;
            }
        }
        if (escaped)
            count++;
    }
    cout << (double)count / 10000 << endl;
}

void reset() {
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            maze[i][j] = 0;
}

bool feasible_dir(int x, int y, int dir) {
    int next_x = x + offset[dir][0];
    int next_y = y + offset[dir][1];

    if (next_x >= 0 && next_x < N && next_y >= 0 && next_y < N
        && maze[next_x][next_y] == 0)
        return true;
    return false;
}

bool is_blocked(int x, int y) {
    for (int d = 0; d < 4; d++) {
        if (feasible_dir(x, y, d))
            return false;
    }
    return true;
}

'IT 프로그래밍 > 객체지향프로그래밍' 카테고리의 다른 글

객체지향프로그래밍 그룹 액티비티 1과 총정리 (0)	2024.04.21
객체지향프로그래밍 1번, 2번, 3번, 4번, 5번, 6번 (0)	2024.04.20
객체지향프로그래밍 16번, 17,번, 18번, 19번, 22번, 23번, 24번 (0)	2024.04.20
객체지향 프로그래밍 13번 , 14번, 15번 (0)	2024.04.20
[C++] 12번 (0)	2024.04.17

현재글객체지향 프로그래밍 25번 , 26번, 28번, 29번, 30번, 31번, 32번, 33번

기술 블로그

x5x6, 거듭제곱 구하는 법, 빈곤 정의, 따배시 강의 요약, 빈곤의 사회학적 정의, 백준 10813, 녹색혁명, 티스토리챌린지, 백준2284번, 오블완, 프로그래밍 예제, 따배시, 빈곤이란 무엇인가?, 빈곤이란, string 설명, C++, 따배시 강의, 빈곤의 원인, strtok기능, 말레이시아 경제,

기술 블로그